第4章图形绘制（续）
强大的绘图功能是MATLAB的鲜明特点之一，它提供了一系列的绘图函数，读者不需要过多的考虑绘图的细节，只需要给出一些基本参数就能得到所需图形。此外，MATLAB还对绘出的图形提供了各种修饰方法，使图形更加美观、精确。
4.3 三维绘制
MATLAB中的三维图形包括三维折线及曲线图、三维曲面图等。创建三维图形和创建二维图形的过程类似，都包括数据准备、绘图区选择、绘图、设置和标注，以及图形的打印或输出。不过，三维图形能够设置和标注更多的元素，如颜色过渡、光照和视角等。
4.3.1 离散数据可视化
绘制二维折线或曲线时，我们可以使用plot命令。与这条命令类似，MATLAB也提供了一个绘制三维折线或曲线的基本命令plot3，其格式是：
plot3(x1,y1,z1,option1,x2,y2,z2,option2,….)
plot3命令以x1，y1，z1所给出的数据分别为x，y，z坐标值，option1为选项参数，以逐点连折线的方式绘制1个三维折线图形；同时，以x2，y2，z2所给出的数据分别为x，y，z坐标值，option2为选项参数，以逐点折线的方式绘制另一个三维折线图形。
plot3命令的功能及使用方法与plot命令的功能及使用方法相类似，它们的区别在于前者绘制出的是三维图形。
plot3命令参数的含义与plot命令的参数含义相类似，它们的区别在于前者多了一个Z方向上的参数。同样，各个参数的取值情况及其操作效果也与plot命令相同。
plot3命令使用的是以逐点连线的方法来绘制三维折线的，当各个数据点的间距较小时，我们也可利用它来绘制三维曲线。
【例4-22】绘制三维曲线示例。
clear,clc
t=0:0.4:40;
figure(1)
subplot(2,2,1);plot3(sin(t),cos(t),t); %画三维曲线
grid
text(0,0,0,’0′); %在x=0,y=0,z=0 处标记”0”
title(‘三维空间’);
xlabel(‘sin(t)’),ylabel(‘cos(t)’),zlabel(‘t’);
subplot(2,2,2);plot(sin(t),t);
grid
title(‘x-z平面’); %三维曲线在x-z 平面的投影
xlabel(‘sin(t)’),ylabel(‘t’);
subplot(2,2,3);plot(cos(t),t);
grid
title(‘y-z平面’); %三维曲线在y-z 平面的投影
xlabel(‘cos(t)’),ylabel(‘t’);
subplot(2,2,4);plot(sin(t),cos(t));
title(‘x-y平面’); %三维曲线在x-y 平面的投影
xlabel(‘sin(t)’),ylabel(‘cos(t)’);
grid
执行程序后，输出如图4-29所示的图形。
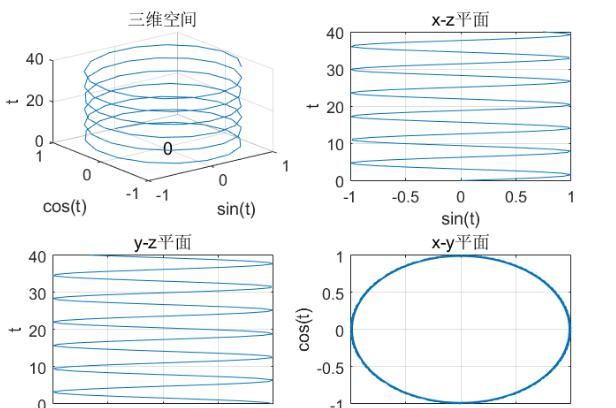
图4-29三维曲线及三个平面上的投影
【例4-23】绘制函数的图形，其中。
clear,clc
x=-5:0.1:5;
y=-5:0.1:5;
[X,Y]=meshgrid(x,y); %将向量x,y指定的区域转化为矩阵X,Y
Z=sqrt(X.^2 Y.^2); %产生函数值Z
mesh(X,Y,Z)
执行程序后，输出如图4-30所示的图形。
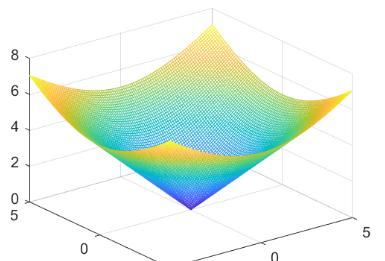
图4-30函数图形
【例4-24】利用plot3绘制三维螺旋线。
clear,clc
t=0:pi/100:7*pi;
x=2*sin(t);
y=3*cos(t);
z=t;
plot3(x,y,z)
执行程序后，输出如图4-31所示图形。
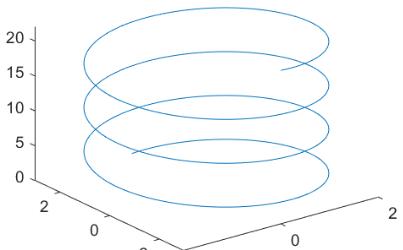
图4-31三维螺旋线图形
【例4-25】利用plot3绘制三维线条图形。
clear,clc
[X,Y]=meshgrid([-4:0.1:4]);
Z=3*X.*(-X.^3-2*Y.^2);
plot3(X,Y,Z,’b’)
执行程序后，输出如图4-32所示的图形。
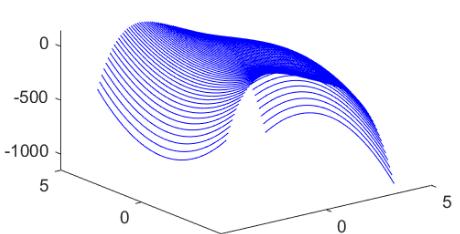
图4-32三维线条图形
在MATLAB中，可用函数surf、surfc来绘制三维曲面图。其调用格式如下：
surf(Z)
%以矩阵Z指定的参数创建一渐变的三维曲面，坐标x = 1:n，y = 1:m，其中[m,n] = size(Z)
surf(X,Y,Z)
%以Z确定的曲面高度和颜色，按照X、Y形成的格点矩阵，创建一渐变的三维曲面。X、Y可以为向量或矩阵，若X、Y为向量，则必须满足m= size(X)，n =size(Y)，[m,n] = size(Z)
surf(X,Y,Z,C)
%以Z确定的曲面高度，C确定的曲面颜色，按照X、Y形成的格点矩阵，创建一渐变的三维曲面
surf(…,’PropertyName’,PropertyValue)
%设置曲面的属性
surfc(…)%采用surfc函数的格式同surf，同时在曲面下绘制曲面的等高线
【例4-26】绘制球体的三维图形。
clear,clc
figure
[X,Y,Z]=sphere(40); %计算球体的三维坐标
surf (X,Y,Z); %绘制球体的三维图形
xlabel(‘x’),ylabel(‘y’),zlabel(‘z’);
title(‘ shading faceted ‘);
执行程序后，输出如图4-33所示的图形。
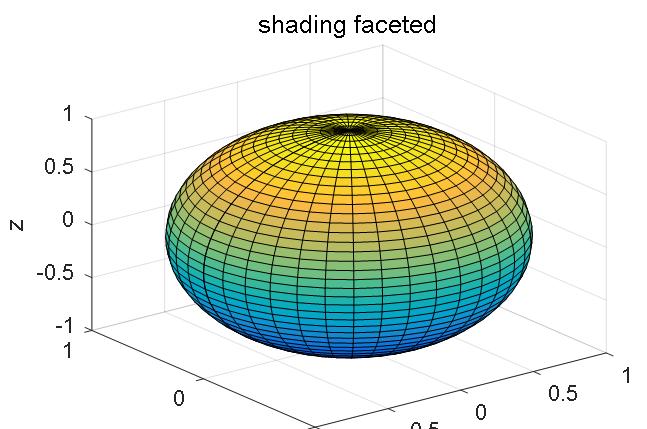
图4-33球体图形
！注意：在图形窗口，需将图形的属性Renderer设置成Painters，才能显示出坐标名称和图形标题。图4-33中，我们看到球面被网格线分割成小块；每一小块可看作是一块补片，嵌在线条之间。这些线条和渐变颜色可以由命令shading来指定，其格式为：
shading faceted
%在绘制曲面时采用分层网格线，为默认值
shading flat
%表示平滑式颜色分布方式；去掉黑色线条，补片保持单一颜色
shading interp
%表示插补式颜色分布方式；同样去掉线条，但补片以插值加色。这种方式需要比分块和平滑更多的计算量
4.3.2 隐藏线的显示和关闭
显示或不显示的网格曲面的隐藏线将对图形的显示效果有一定的影响。MATLAB提供了相关的控制命令hidden，调用这种命令的格式是：
hidden on %去掉网格曲面的隐藏线；
hidden off %显示网格曲面的隐藏线。
【例4-27】绘出有隐藏线和无隐藏线的函数的网格曲面。
clear,clc
x=-7:0.4:7;
y=x;
[X,Y]=meshgrid(x,y);
R=sqrt(X.^2 Y.^2) eps;
Z=cos(R)./R;
subplot(1,2,1),mesh(X,Y,Z)
hidden on,grid on
title(‘hidden on’)
axis([-10 10 -10 10 -1 1])
subplot(1,2,2),mesh(X,Y,Z)
hidden off,grid on
title(‘hidden off’)
axis([-10 10 -10 10 -1 1])
执行程序后，输出如图4-34所示的图形：
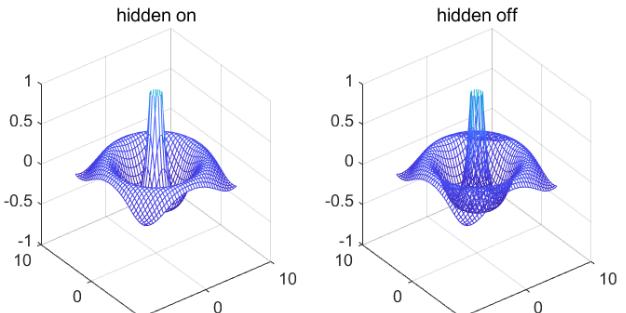
图4-34有无隐藏线的函数网格曲面图
4.3.3 三维绘图的实际应用
【例4-28】在一丘陵地带测量高度，x和y方向每隔50米测一个点，得高度见表4-2，试拟合一曲面，确定合适的模型，并由此找出最高点和该点的高度。
表4-2高度数据
100
200
300
400
100
536
597
524
278
200
598
612
530
378
300
580
574
498
312
400
562
526
452
234
x=[100 100 100 100 200 200 200 200 300 300 300 300 400 400 400 400];
y=[100 200 300 400 100 200 300 400 100 200 300 400 100 200 300 400];
z=[536 597 524 378 598 612 530 378 580 574 498 312 562 526 452 234];
xi=100:10:400;
yi=100:10:400;
[X,Y]=meshgrid(xi,yi);
H=griddata(x,y,z,X,Y,’cubic’);
surf(X,Y,H);
view(-112,26);
hold on;
maxh=vpa(max(max(H)),6)
[r,c]=find(H>=single(maxh));
stem3(X(r,c),Y(r,c),maxh,’fill’)
title(‘高度曲面’)
执行程序后，输出如图4-35所示的高度曲面图像。同时得到最高点为：
maxh =616.113
即该丘陵地带高度最高点为616.113。
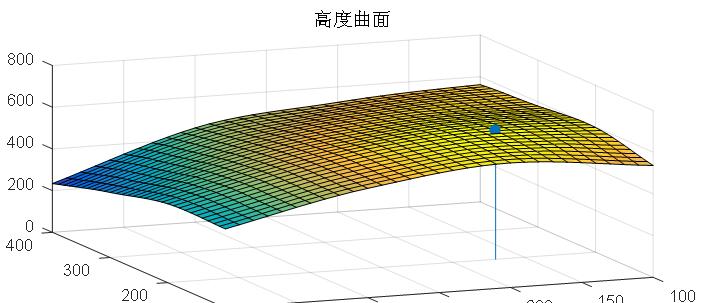
图4-35拟合的高度曲面
