01
引言
例如,在二项分布中,我们常常用到E(X)=np,D(X)=np(1-p)等二级结论。对这些公式的证明,涉及和式变换、组合数、数列、二项式定理等非常丰富的内容。下面我们整理几个推导过程。

02
几个推导
注:本着针对高中学习的原则,文中出现的所有随机变量均为离散型随机变量。
2.1 超几何分布的期望公式

这个推导的亮点在于对排列组合公式实际意义的说明。通过说明实际意义来证明命题的方法在其他一些排列组合题目中也有体现,往往能够非常轻巧的处理看起来毫无头绪的问题,值得读者朋友们注意。
同时,证明第三行中用到的组合数变形是简单常用的,在后面的推导中也会用到。

2.2 二项分布的期望公式
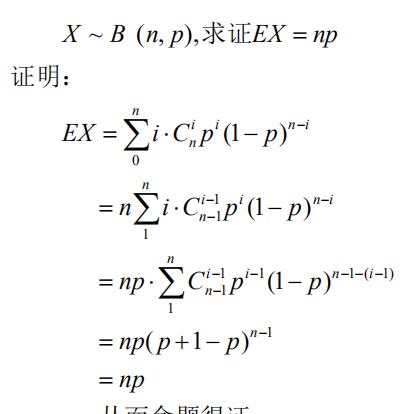
在对这个公式的推导中,我们的线索就是“二项式定理”的形式,对方差的推导也是如此。

2.3 二项分布的方差公式
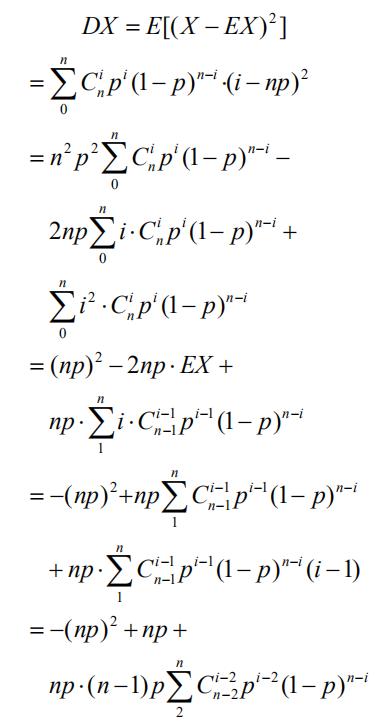
这个推导反复运用组合数变形向二项式形式靠拢,有一定的技巧性。

2.4 用期望表出方差
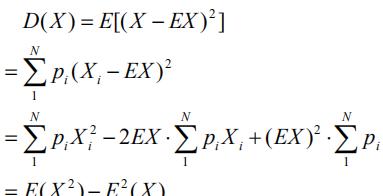

03
总结
对于文中涉及的这些公式,掌握它们的推导并不在考试要求的范围之内。但是这些推导过程中蕴含着非常精妙的数学思想与技巧,值得我们去考察。例如,向二项式形式靠拢就体现着“转化与化归”的数学思想。了解这些推导,一方面可以加深对这些公式的理解记忆,另一方面也有利于体会一些数学方法的应用过程。
THE
END