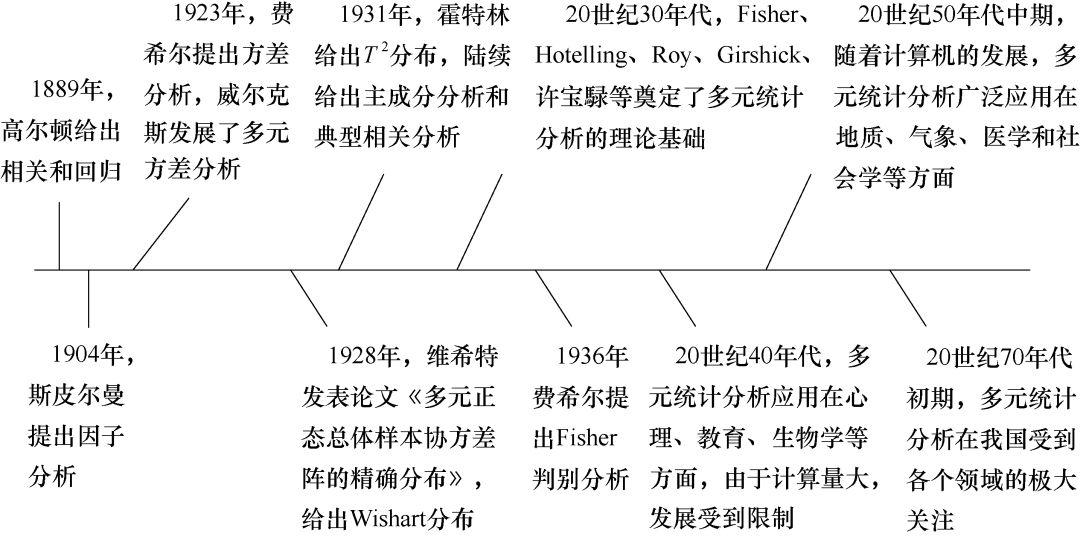
一、什么是多元统计分析一元统计分析是研究一个随机变量统计规律的学科,有其理论和现实的局限性。多元统计分析,顾名思义,是对多维随机变量进行分析和研究,研究它们之间的相互依赖关系以及内在统计规律性的统计学科。如何同时对多个随机变量的观测数据进行有效的分析和研究?假如把多个随机变量分开分析,每个随机变量用一元统计分析方法研究,就不会清楚多个变量之间的相关性,会丢失信息,不易获得好的研究结果。科学的方法是对多个变量同时进行分析研究,采用多元统计分析方法,通过同时对多个随机变量观测数据的分析,来研究变量之间的相互关系以及揭示这些变量内在的变化规律。法国著名数学家庞加来(J.H.Poincaré,1854—1912年)说过,“如果我们想预测数学的未来,那么正确的途径是研究其历史与现状”。史学研究是任何学科永恒的研究主题,多元统计学自然不能例外,统计学史上曾涌现多位杰出的多元统计学家。首先涉足多元分析方法的是英国统计学家高尔(F.Galton),他于1889年把双变量的正态分布方法运用于传统的统计学,他于六年中测量了近万人的“身高、体重、阔度、呼吸力、拉力和压力、手击的速率、听力、视力、色觉及个人的其他资料”,在探究这些数据内在联系的过程中提出了今天在自然科学和社会科学领域中广泛应用的“相关”思想,创立了线性回归,他的学生皮尔逊(K.Pearson)受其影响,给出积矩相关系数、复相关等研究多个变量之间关系的概念和方法。其后,斯皮尔曼(C.E.Spearman)提出对多维变量进行降维的因子分析法,费希尔(R.A.Fisher)提出方差分析和判别分析,美国的威尔克(S.S.Wilks)发展了多元方差分析,美国的霍特林(H.Hotelling)确定了主成分分析和典型相关分析。到20世纪前半叶,多元分析理论基础基本确立,1928年英国的维希特(J.Wishart)发表论文《多元正态总体样本协方差阵的精确分布》,是学术界公认的多元统计分析理论研究的开端。R.A.Fisher、H.Hotelling、S.N.Roy、M.A.Girshick、许宝騄等人做了一系列奠基的工作,使多元统计分析在理论上得迅速的发展,在许多领域中有了实际应用。21世纪初,人们获得的数据正以前所未有的速度急剧增加,产生了很多超大型数据库,遍及超级市场销售、银行存款、天文学、粒子物理、化学、医学以及政府统计等领域,多元统计与人工智能、数据库技术相结合,已在经济、商业、金融、天文等行业得到成功应用。为了更清楚地了解多元统计分析史的发展脉络,我们给出下图描述多元分析的发展。
二、多元统计分析的主要内容和方法
多元统计分析是应用数理统计学来研究多变量(多指标)问题的理论和方法,是统计学的一个重要分支。它是一元统计学的推广和发展,是一门具有很强应用性的课程,在自然科学和社会科学等领域中得到广泛的应用,包括了很多非常有用的数据处理方法。英国著名统计学家肯德尔(M.G.Kendall)先后出版了《多元分析》《统计理论入门》《高等统计学理论》《等级相关方法》《时间序列》《几何概率》《统计学和概率史研究》等著作。Kendall在MultivariateAnalysis(1983年)一书中把多元分析所研究的内容和方法概括为以下几个方面。
1.多元统计分析的理论基础
多元统计分析的理论基础包括多维随机向量及多维正态随机向量,以及由此定义的各种多元统计量,推导它们的分布并研究其性质,研究它们的抽样分布理论。这些是统计估计和假设检验的基础,也是多元统计分析的理论基础。
2.多元数据的统计推断
多元数据的统计推断主要研究多元正态分布的均值向量和协差阵的估计和假设检验等问题。
3.简化数据结构
简化数据结构主要研究降维问题。例如,通过变量变换等方法使相互依赖的变量变成互不相关的变量;或把高维空间的数据投影到低维空间,使问题得到简化而损失的信息又不太多。主成分分析、因子分析、对应分析等多元统计方法就是这样的一类方法。
4.变量间的相互联系
①相互依赖关系:分析一个或几个变量的变化是否依赖于另一些变量的变化。如果是,建立变量间的定量关系式,并用于预测或控制———回归分析。
②变量间的相互关系:分析两组变量间的相互关系———典型相关分析等。
③ 定性变量间的相互关系:对应分析等。
5.分类与判别
对所考察的对象(样品点或变量)按相似程度进行分类(或归类)。聚类分析和判别分析等方法是解决这类问题的统计方法。
上述内容可由下表进行概括,从表中可知一种方法有时会解决多个问题。
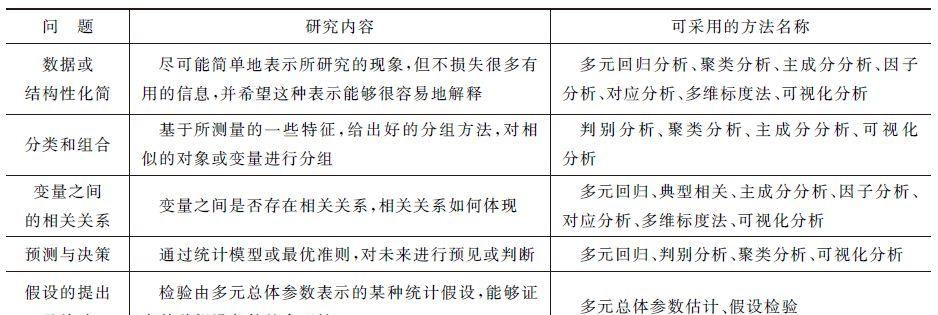
例如,在考查大学生的学习情况时,需了解学生的几个主要课程的考试成绩。下表给出从某大学某学院随机抽取的100名学生中6门主要课程的期末考试成绩。
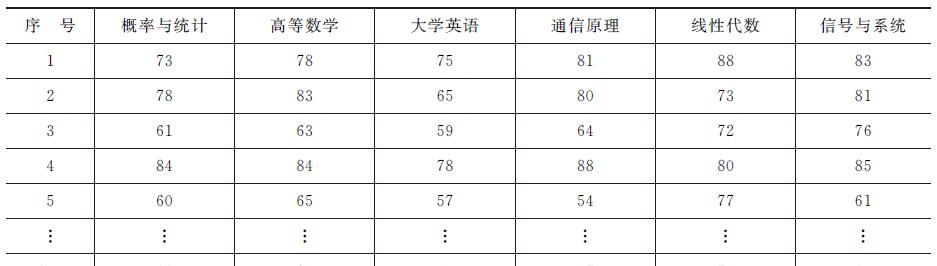
如果使用一元统计方法,就要把多门课程分开分析,每次分析处理一门课的成绩,这样处理,忽视了课程之间可能存在的相关性,丢失信息太多,使得分析的结果不能客观全面地反映学生的学习情况。如果使用多元分析方法,可以同时对多门课程成绩进行分析。例如:可以运用典型相关、对应分析、图形可视化了解这些课程之间的相互关系、相互依赖性等;可以运用主成分分析、因子分析研究影响成绩的主要因素,用主要因素(综合指标)来比较学生学习成绩的好坏;可以运用聚类分析对学生进行分类,从而对不同类别的学生分析成绩构成,制订相应学习计划;可以运用多元回归分析根据一些课程成绩预测其他课程成绩;可以运用判别分析根据一些课程成绩判别学生类别。上面提到的典型相关、对应分析、图形可视化、主成分分析、因子分析、聚类分析、判别分析等都属于多元统计分析的研究内容。