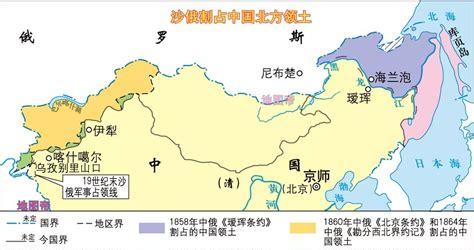
怎么求函数值域?
1.一、配方法。
将函数配方成顶点式的格式,再根据函数的定义域,求得函数的值域。(画一个简易的图能更便捷直观的求出值域。)

??
2/9
二、常数分离
这一般是对于分数形式的函数来说的,将分子上的函数尽量配成与分母相同的形式,进行常数分离,求得值域。
3/9
三、逆求法
对于y=某x的形式,可用逆求法,表示为x=某y,此时可看y的限制范围,就是原式的值域了。
4/9
换元法
对于函数的某一部分,较复杂或生疏,可用换元法,将函数转变成我们熟悉的形式,从而求解
5/9
五、单调性
可先求出函数的单调性(注意先求定义域),根据单调性在定义域上求出函数的值域。
6/9
六、基本不等式
根据我们学过的基本不等式,可将函数转换成可运用基本不等式的形式,以此来求值域。
7/9
七、数形结合
可根据函数给出的式子,画出函数的图形,在图形上找出对应点求出值域
8/9
八、求导法
求出函数的导数,观察函数的定义域,将端点值与极值比较,求出最大值与最小值,就可的到值域了。
9/9
九、判别式法
将函数转变成 ****=0 的形式,再用解方程的方法求出要满足的条件,求解即可。
注意事项
不知道是否有表述清楚,可图片里的例子进行理解。
方法很多,重在理解,才能掌握
求值域的几种方法?
1.1.直接法:从自变量的范围出发,推出值域。
2.观察法:对于一些比较简单的函数,可以根据定义域与对应关系,直接得到函数的值域。
3.配方法:(或者说是最值法)求出最大值还有最小值,那么值域就出来了。
例题:y=x^2+2x+3x∈【-1,2】
先配方,得y=(x+1)^2+1
∴ymin=(-1+1)^2+2=2
ymax=(2+1)^2+2=11
4.拆分法:对于形如y=cx+d,ax+b的分式函数,可以将其拆分成一个常数与一个分式,再易观察出函数的值域。
5.单调性法:y≠ca.一些函数的单调性,很容易看出来。或者先证明出函数的单调性,再利用函数的单调性求函数的值域。
6.数形结合法,其题型是函数解析式具有明显的某种几何意义,如两点的距离公式直线斜率等等,这类题目若运用数形结合法,往往会更加简单,一目了然,赏心悦目。
7.判别式法:运用方程思想,根据二次方程有实根求值域。
8.换元法:适用于有根号的函数
例题:y=x-√(1-2x)
设√(1-2x)=t(t≥0)
∴x=(1-t^2)/2
∴y=(1-t^2)/2-t
=-t^2/2-t+1/2
=-1/2(t+1)^2+1
∵t≥0,∴y∈(-∝,1/2)
9:图像法,直接画图看值域
这是一个分段函数,你画出图后就可以一眼看出值域。
10:反函数法。求反函数的定义域,就是原函数的值域。
例题:y=(3x-1)/(3x-2)
先求反函数y=(2x-1)/(3x-3)
明显定义域为x≠1
所以原函数的值域为y≠1