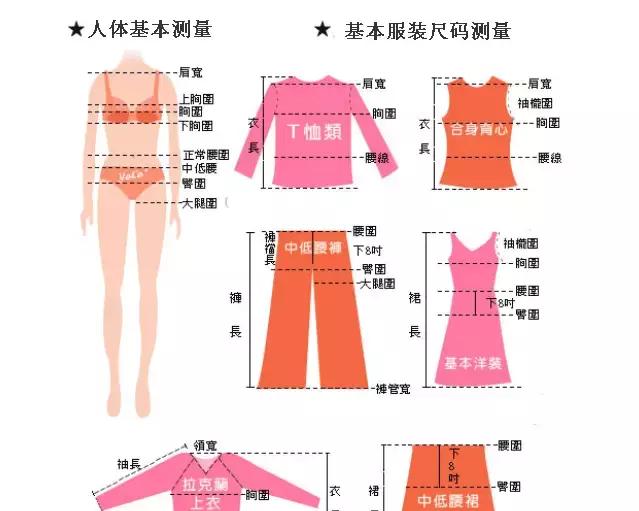
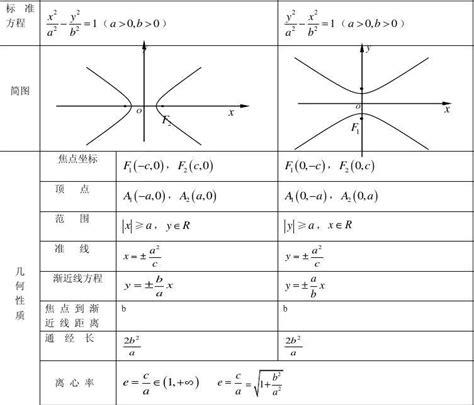
焦点在y轴的推导公式?
1.设点M是焦点在y轴上的双曲线上任意一点,焦距|F1F2|=2c,| |MF1| – |MF2| | =2a,其中c>a>0
那么焦点坐标为下焦点F1(0,-c),上焦点F2(0,c)
所以有:|MF1|=根号[x??+(y+c)??] ,|MF2|=根号[x??+(y-c)??]
则由 |MF1| – |MF2| =±2a可得:
根号[x??+(y+c)??] – 根号[x??+(y-c)??]=±2a
移项得:根号[x??+(y+c)??] =±2a+根号[x??+(y-c)??]
两边平方得:
{根号[x??+(y+c)??]}?? ={±2a+根号[x??+(y-c)??]}??
x??+(y+c)??=4a?? ± 4a根号[x??+(y-c)??] + x??+(y-c)??
4cy=4a?? ± 4a根号[x??+(y-c)??]
cy-a??=± a根号[x??+(y-c)??]
再次两边平方得:
c??y??-2cya??+a的4次幂=a??[x??+(y-c)??]
c??y??-2cya??+a的4次幂=a??x??+a??y??-2cya??c+a??c??
(c??-a??)y??-a??x??=a??c??-a的4次幂
即(c??-a??)y??-a??x??=a??(c??-a??) (*)
由于c>a>0,所以不妨令c??-a??=b??,b>0
上述(*)式可化为:b??y??-a??x??=a??b??
则可得:y??/a?? -x??/b??=1
这就是所求的焦点在y轴的双曲线的标准方程