椭圆周长怎么算?
我们知道圆的周长和直径成正比,比值为圆周率,只要知道圆的直径,很容易就能算出圆的周长。然而,椭圆的周长却很难计算出来,因为椭圆的周长无法通过初等函数进行表示。不过,存在一些能够比较准确地计算出椭圆周长的近似初等公式。
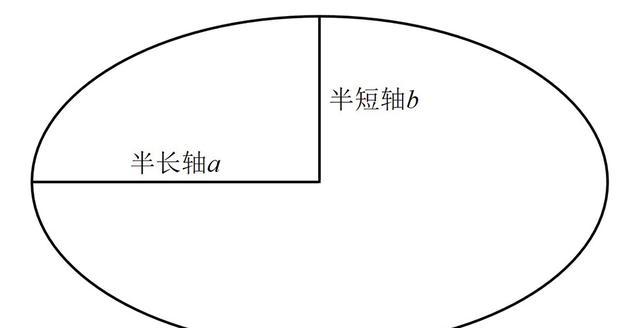
圆的特点是圆上的任意一点到圆心的距离都是固定的,这个距离我们称之为半径。但椭圆没有像圆一样拥有一个始终是常数的半径,取而代之的是定义了两个参数:长轴和短轴。长轴过椭圆的两个焦点,是椭圆上最长的弦,从中心到端点的线段被称为半长轴(用字母a表示)。短轴垂直平分于长轴,从中心到端点的线段被称为半短轴(用字母b表示)。
对于偏心率(用字母e表示)不是特别高的椭圆,也就是说形状不是特别的椭圆,可以通过求出椭圆的平均半径来计算周长。只要求出椭圆的平均半径,我们就可以像计算圆的周长那样来近似计算椭圆的周长:C=2πr。由于椭圆的平均半径为:r=√[(a^2+b^2)/2],所以椭圆的近似周长为:
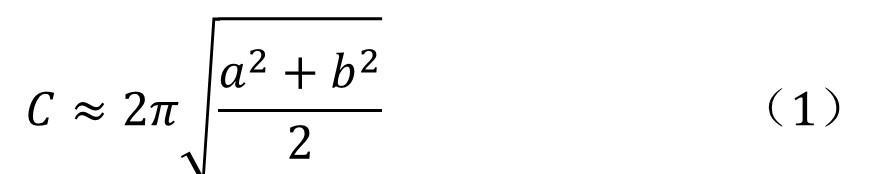
如果半长轴没有超过半短轴的3倍(a/b<3),则这种近似方法计算出的椭圆周长的误差小于5%。
印度数学家拉马努金提出了两个更好的椭圆周长近似初等公式:
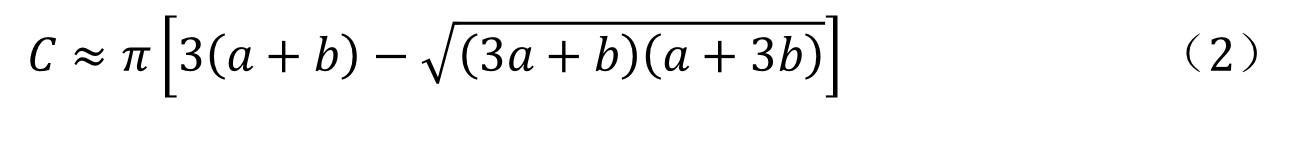

公式(3)的计算精度更高,可以用22/7来近似替代圆周率,误差小于0.05%。
此外,椭圆周长的精确公式可以用无穷级数进行表达:
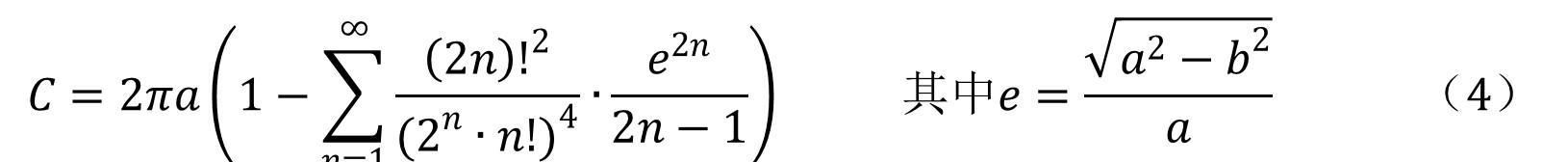
由于是无穷级数,我们无法算出其精确值,只能通过计算足够多的项数来提高计算精度。
总之,在计算椭圆周长时,根据所需的精度来选择相应的近似公式。
椭圆的周长和面积公式是什么?
1.椭圆的面积公式:S=π×a×b(其中a,b分别是椭圆的长半轴、短半轴的长)或S=π×A×B/4(其中A、B分别是椭圆的长轴、短轴的长)。
椭圆的面积公式可利用仿射变换法、积分法等方法求得,此处以仿射变换法为例推到椭圆的面积公式:从椭圆方程可知椭圆是一个被“压缩”了的圆,则可设椭圆方程为:(x/a)^2+(y/b)^2=1
令:x’=x,y’=y*a/b,
我们就可以在新的坐标系中得到一个圆:x’^2+y’^2=a^2
新坐标系其实是一个在y方向等比(比例为a/b)拉长了的坐标系,这样在新坐标系得到面积 S=π*a^2后,再乘以比例b/a后得到:S=π×a×b 就是所求答案
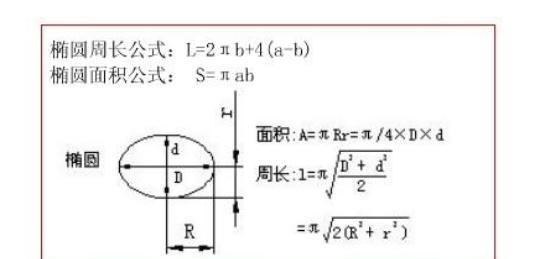
椭圆周长公式:L=2πb+4(a-b)(其中a,b分别是椭圆的长半轴、短半轴的长)。