什么是虚数?
1.从幼儿园开始,老师就会叫我们认识字母、拼音、图像等等,这些都是为我们的学习奠定基础。
在更高级的学习里面,最重要的就是掌握某一概率或者含义,知道了什么意思才能够去解决或者是继续开发新事物。
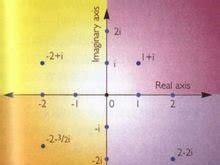
在化学、数学、物理、语文上面都是很考验学者对某一专业词语的理解能力的,就比如数学里面的虚数,它定义是什么?
在数学里,将偶数指数幂是负数的数定义为纯虚数,虚数是没有正负可言的和虚数相对的就是实数,还有复数,这些词语在数学里面都是很重要的的概率词之一。
2.虚数:
1、平方为负数的数。
2、所有的虚数都是复数。
3、“虚数”这个名词是由十七世纪著名数学家笛卡尔创制。
4、在数学里,将偶指数幂是负数的数定义为纯虚数。
5、所有的虚数都是复数。
6、虚数没有算术根。
7、实数和虚数组成的一对数在复数范围内看成一个数,起名为复数。
8、虚数没有正负可言。
9、不是实数的复数,即使是纯虚数,也不能比较大小。
什么是虚数和复数?
1.负数开平方,在实数范围内无解。 数学家们就把这种运算的结果叫做虚数,因为这样的运算在实数范围内无法解释,所以叫虚数。 实数和虚数组成的一对数在复数范围内看成一个数,起名为复数。 于是,实数成为特殊的复数(缺序数部分),虚数也成为特殊的复数(缺实数部分)。 虚数单位为i, i即根号负1。 3i为虚数,即根号(-3), 即3×根号(-1) 2+3i为复数,(实数部分为2,虚数部分为3i) 复数和虚数不一样,形如a+bi的数。
式中a,b 为实数,i是 一个满足i2=-1的数,因为任何实数的平方不等于-1,所以i不是实数,而是实数以外的新的数。
在复数a+bi中,a 称为复数的实部,b称为复数的虚部,i称为虚数单位。当虚部等于零时,这个复数就是实数;当虚部不等于零时,这个复数称为虚数,虚数的实部如果等于零,则称为纯虚数。由上可知,复数集包含了实数集,因而是实数集的扩张.
2.虚数是指所有含有字母i的数,数学上特别定义i??=-1,因为实数范围内任何数的平方都不等于负一,所以i和含有i的数字一律都叫虚数,例如3i,2+5i,-0.5i都是虚数。虚数和实数统称为复数,复数是最大的范围,所有的实数都是复数,所有的虚数也都是复数。
3.在数学中,虚数就是形如a+b*i的数,其中a,b是实数,且b≠0,i?? = – 1。虚数这个名词是17世纪著名数学家笛卡尔创立,因为当时的观念认为这是真实不存在的数字。
后来发现虚数a+b*i的实部a可对应平面上的横轴,虚部b与对应平面上的纵轴,这样虚数a+b*i可与平面内的点(a,b)对应。
可以将虚数bi添加到实数a以形成形式a + bi的复数,其中实数a和b分别被称为复数的实部和虚部。一些作者使用术语纯虚数来表示所谓的虚数,虚数表示具有非零虚部的任何复数。
我们把形如z=a+bi(a,b均为实数)的数称为复数,其中a称为实部,b称为虚部,i称为虚数单位。当虚部等于零时,这个复数可以视为实数;当z的虚部不等于零时,实部等于零时,常称z为纯虚数。
复数域是实数域的代数闭包,即任何复系数多项式在复数域中总有根。 复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受。