八年级数学想要考高分,每一个考点知识都不可以疏忽,今天给大家梳理了一份初二数学下册二次根式易错题汇总,出错率达90%。从基础知识点到进阶知识难点,让学生逐步巩固知识,掌握高分解题思路与技巧后学会举一反三,二次根式不再害怕,数学成绩遥遥领先。
1、当a>1时,化简
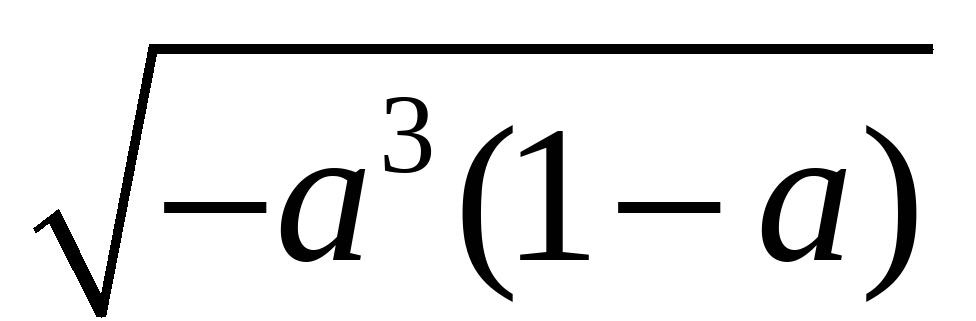 的结果是___________2、把
的结果是___________2、把
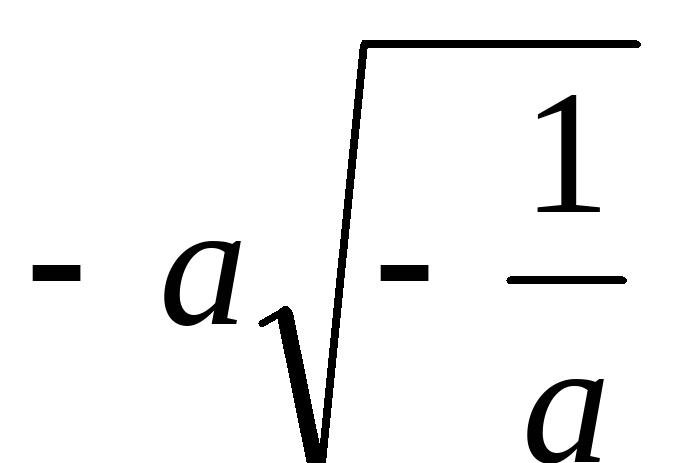 根号外的因式移入根号内的结果是_____________3、若k、b是一元二次方程x2 px-│q│=0的两个实根(kb≠0),在一次函数y=kx b中,y随x的增大而增大,则一次函数的图像一定经过_____________________4、已知Rt△ABC的两条边长都是方程x2-6x 8=0的根,则Rt△ABC的第三边可能是 5、已知关于x的一元二次方程(m﹣1)x2 x 1=0没有实数根,则m的取值范围是 ______ .6、已知关于x的方程
根号外的因式移入根号内的结果是_____________3、若k、b是一元二次方程x2 px-│q│=0的两个实根(kb≠0),在一次函数y=kx b中,y随x的增大而增大,则一次函数的图像一定经过_____________________4、已知Rt△ABC的两条边长都是方程x2-6x 8=0的根,则Rt△ABC的第三边可能是 5、已知关于x的一元二次方程(m﹣1)x2 x 1=0没有实数根,则m的取值范围是 ______ .6、已知关于x的方程
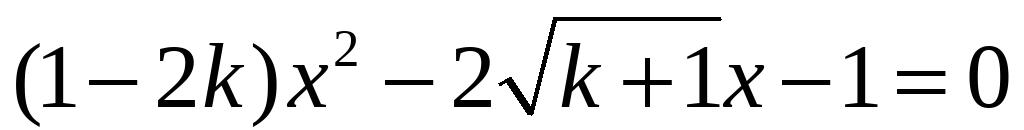 有两个不相等的实数根,则k的取值范围是
有两个不相等的实数根,则k的取值范围是
7、若
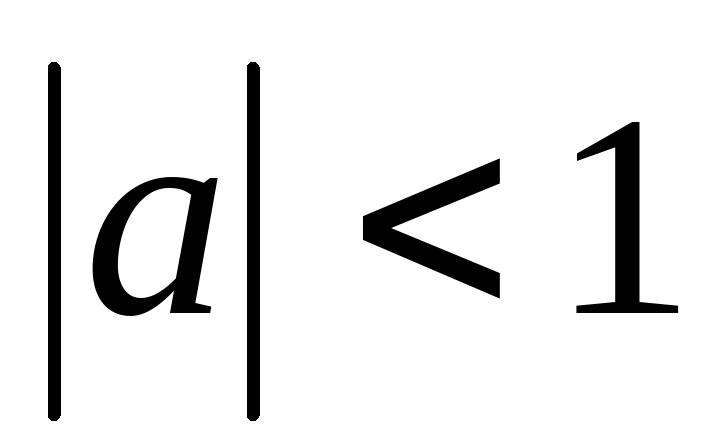 ,则
,则
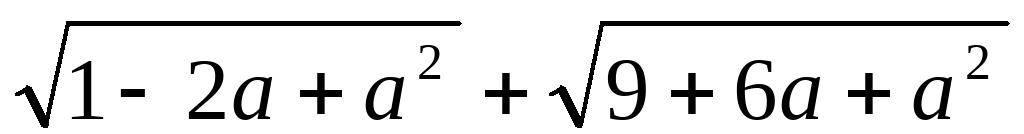 的结果是( )(A)-2a-2 (B)2a 2 (C)4 (D)-48、化简
的结果是( )(A)-2a-2 (B)2a 2 (C)4 (D)-48、化简
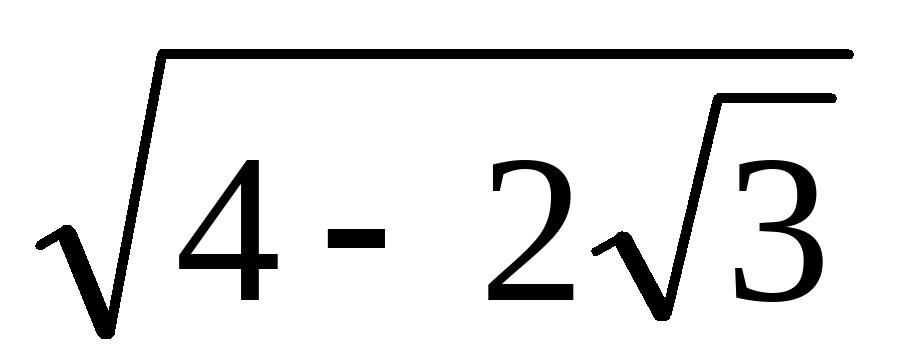 的结果是( )(A)
的结果是( )(A)
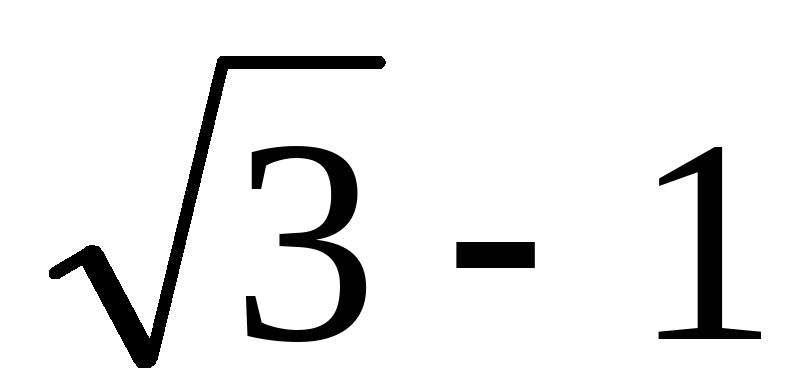 (B)
(B)
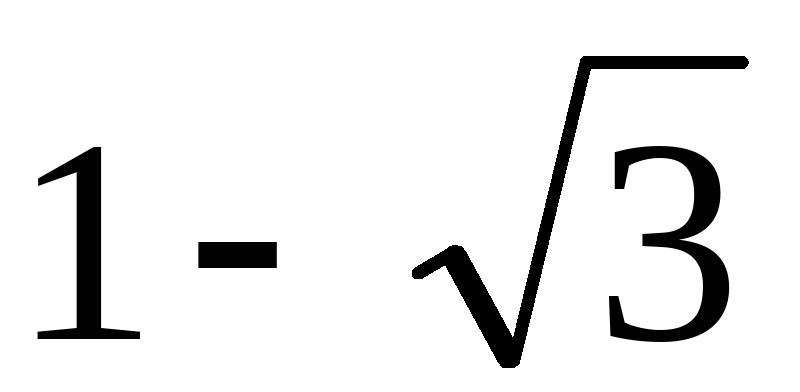 (C)
(C)
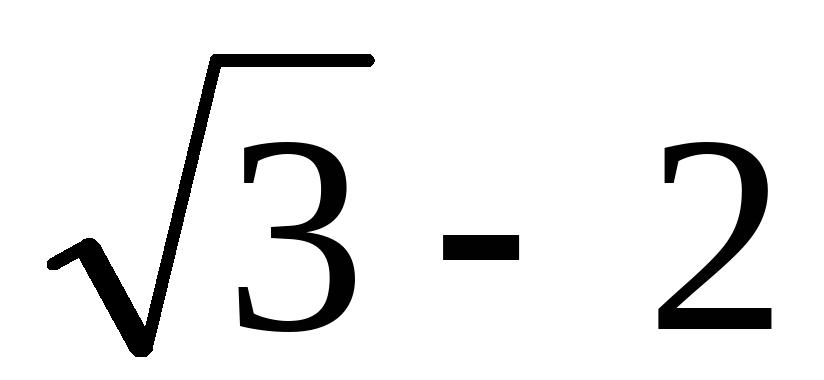 (D)
(D)
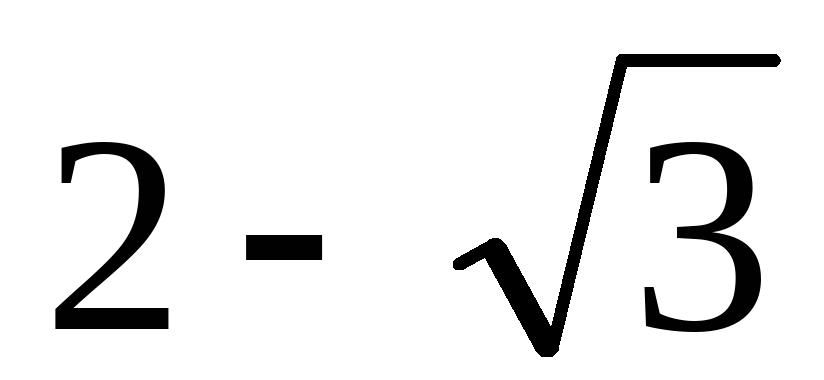 9、如果
9、如果
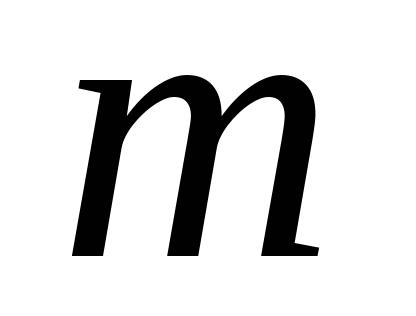 <0,那么化简
<0,那么化简
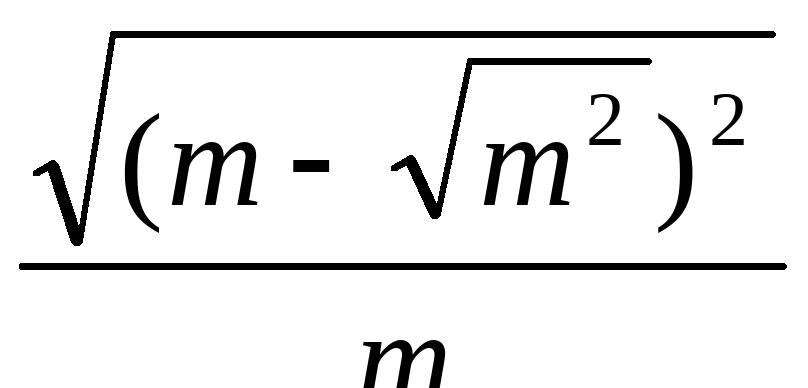 的结果是( )(A)-2 (B)1 (C)-1 (D)210、把下列各式分母有理化:(1).
的结果是( )(A)-2 (B)1 (C)-1 (D)210、把下列各式分母有理化:(1).
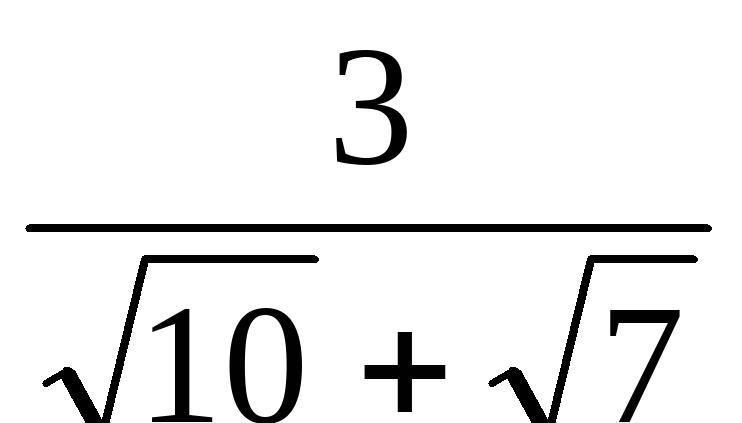 (2).
(2).
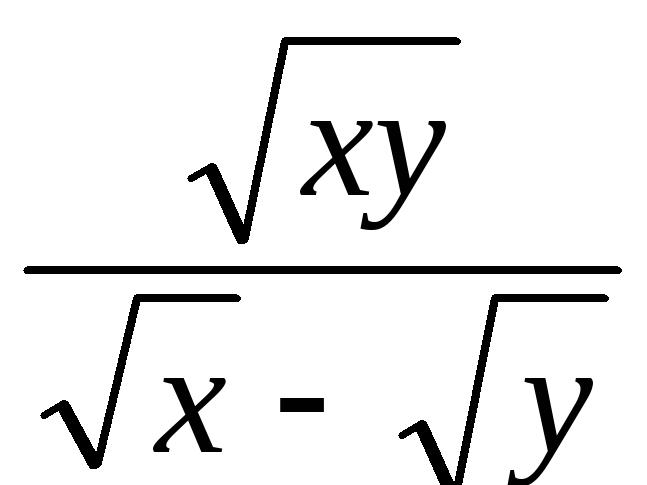 (4).
(4).
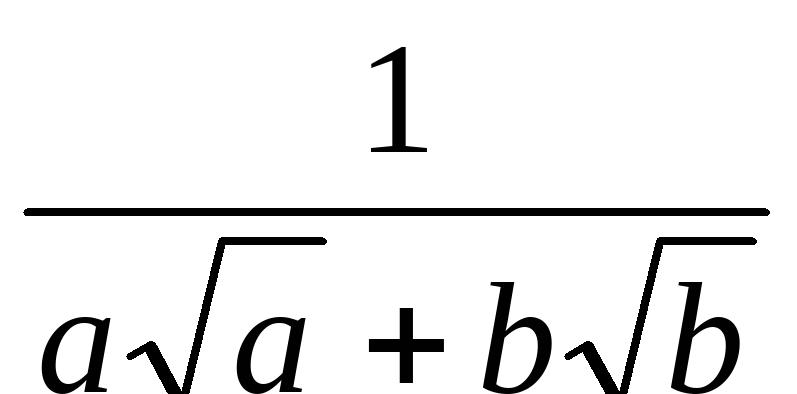 (a≠b)(5).
(a≠b)(5).
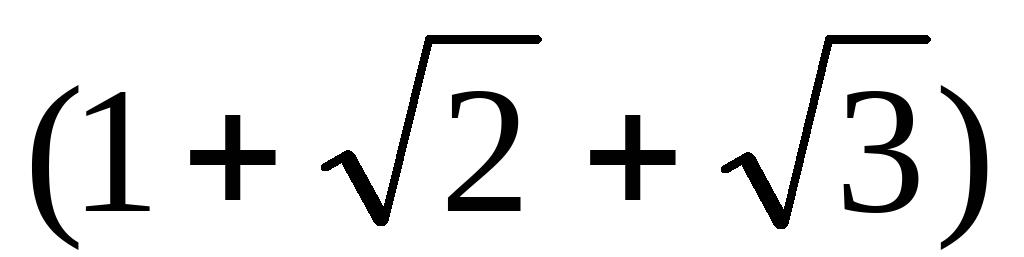 (
(
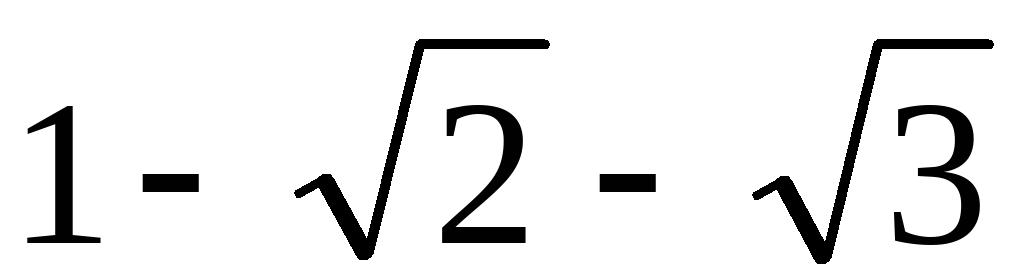 )(6).
)(6).
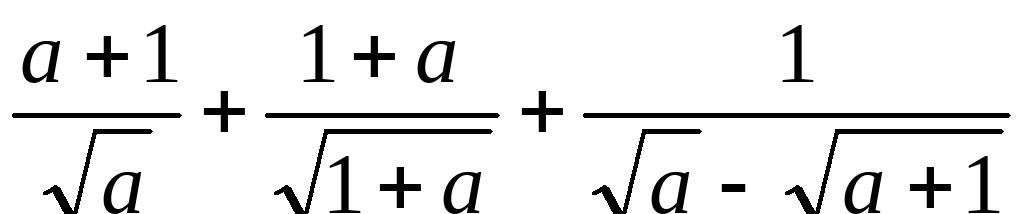 11、化简:(1).
11、化简:(1).
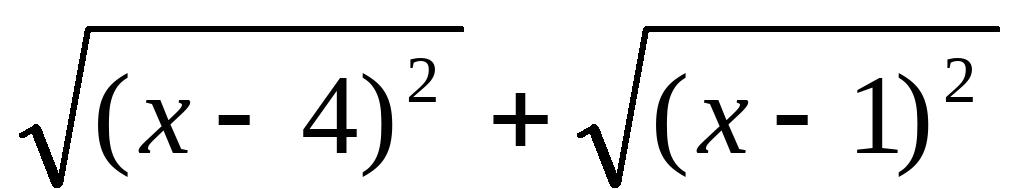 (1<x<4) (2).(x y)
(1<x<4) (2).(x y)
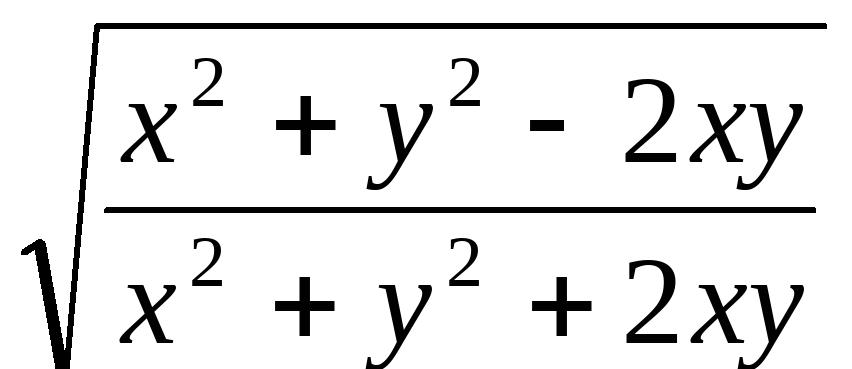 (x<y<0)12、已知:x=
(x<y<0)12、已知:x=
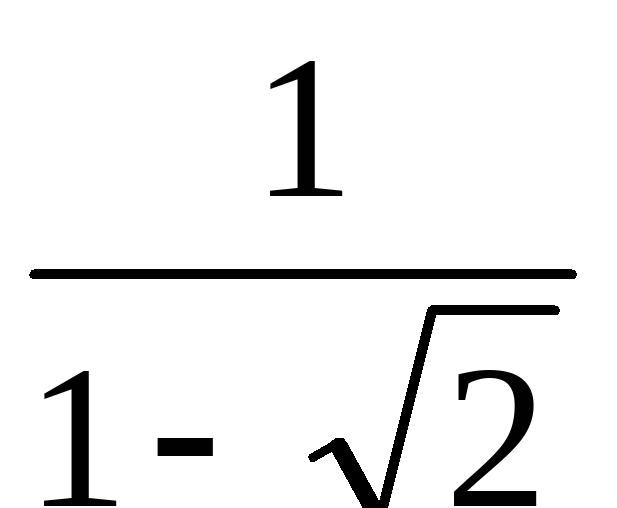 ,求代数式3-
,求代数式3-
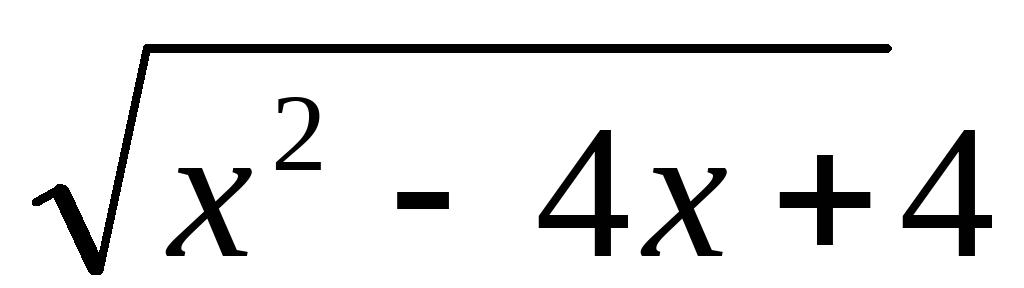 的值13、已知
的值13、已知
 =
=
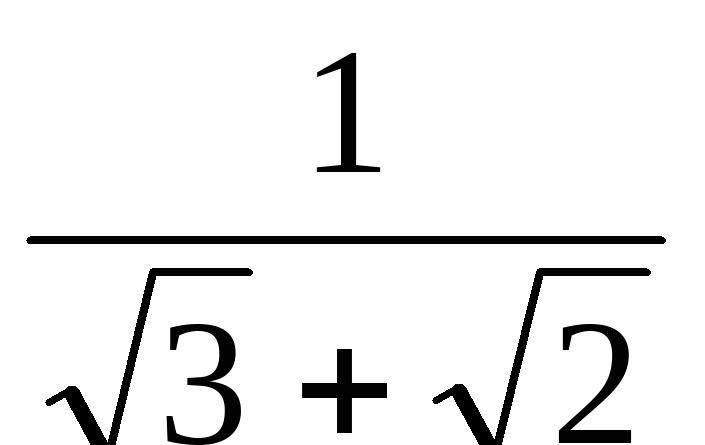 ,求
,求
 的值。14、已知:
的值。14、已知:
 ,
,
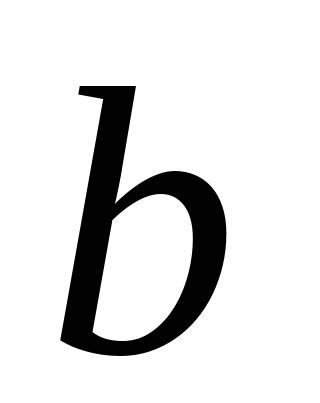 为实数,且
为实数,且
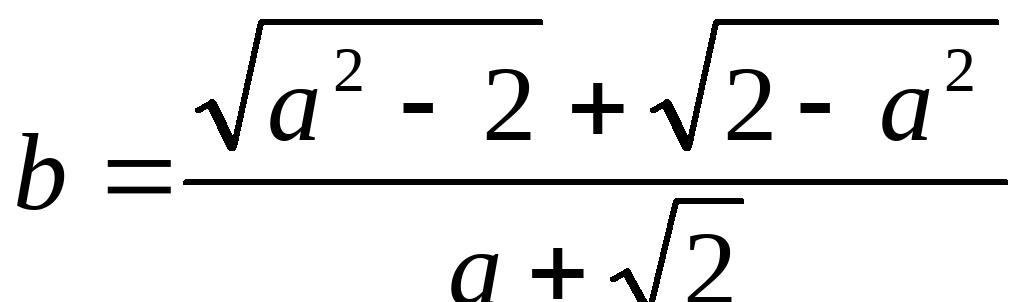 。求
。求
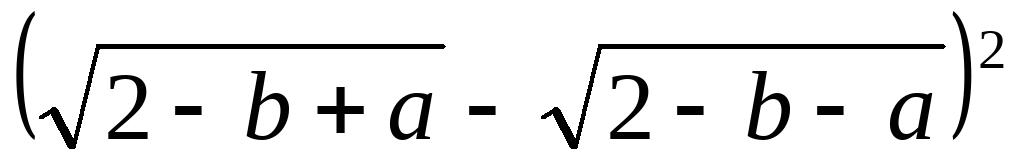 的值。15、计算:(1)
的值。15、计算:(1)
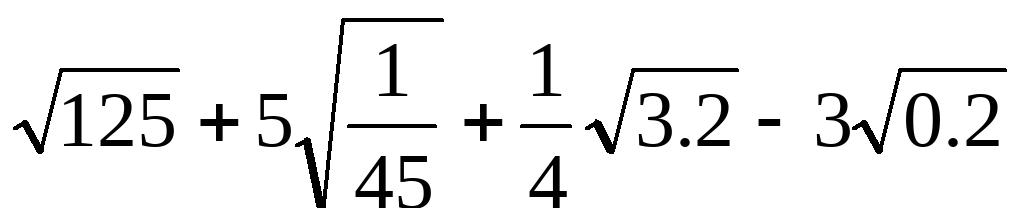 (2)
(2)
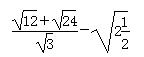 (3)
(3)
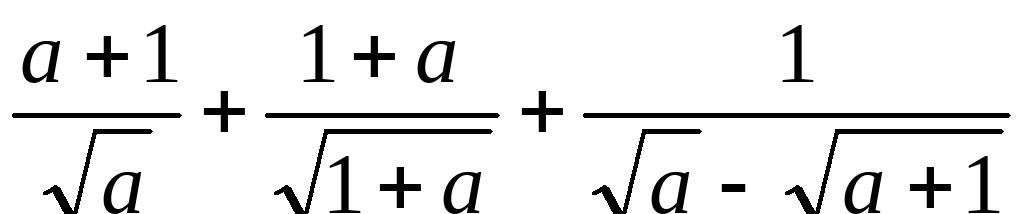 (4)
(4)
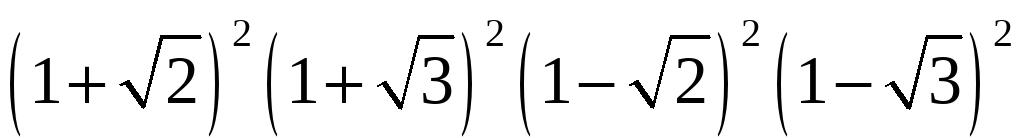 (5)
(5)
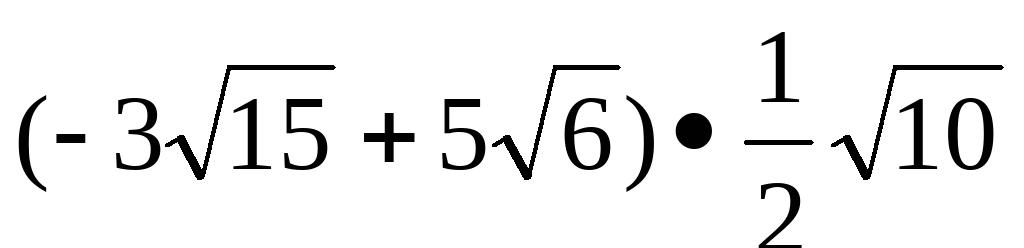 (6)
(6)
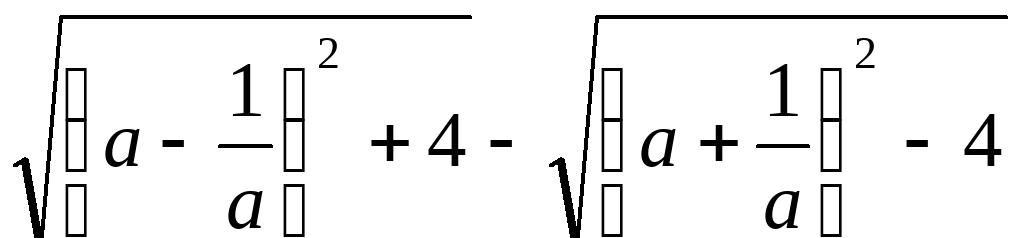
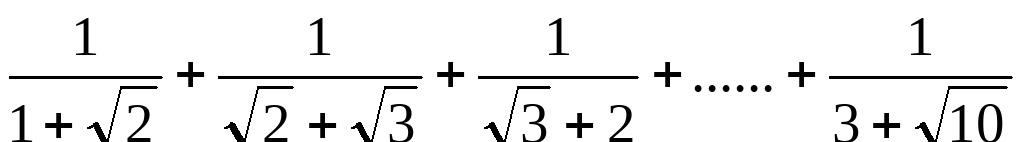 (7)当a=
(7)当a=
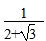 时,求
时,求
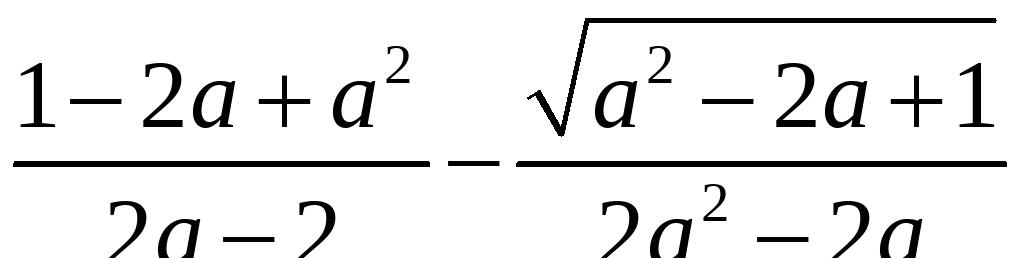 的值16、已知
的值16、已知
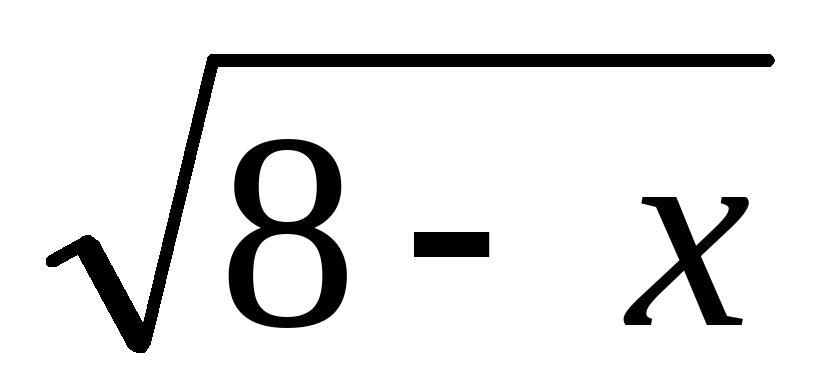
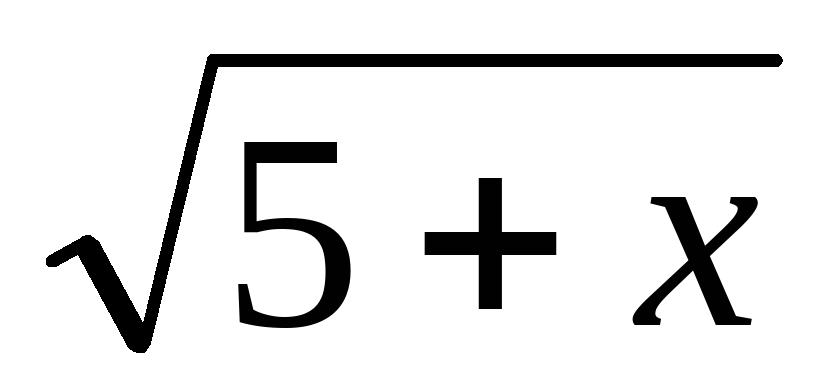 =5,求
=5,求
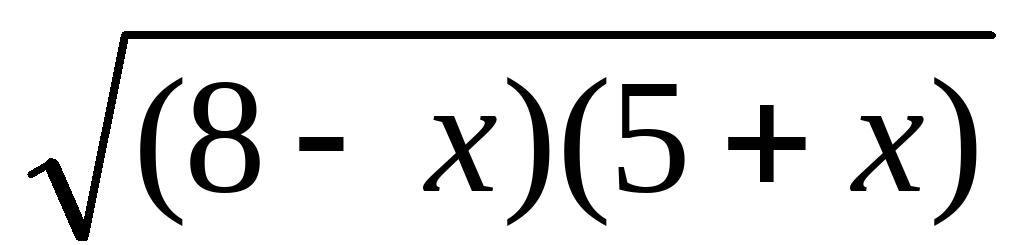 的值17、已知
的值17、已知
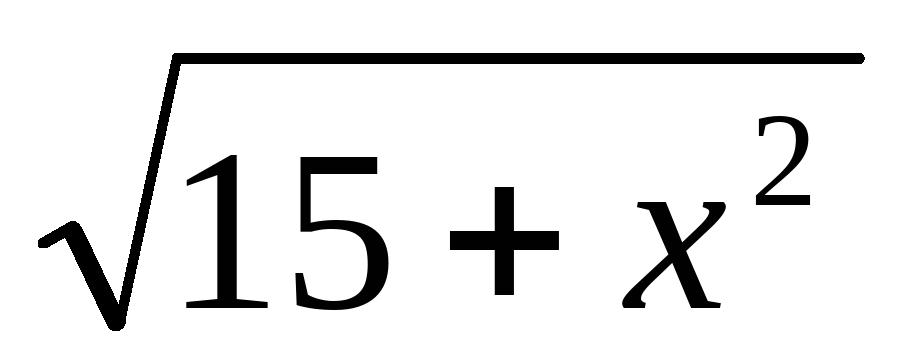 -
-
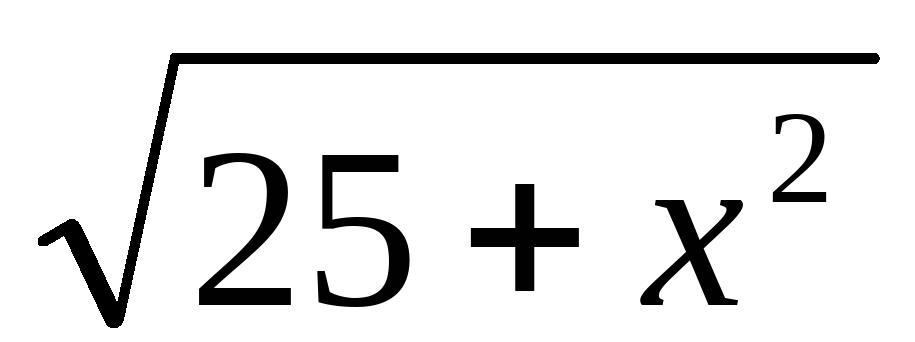 =2,求
=2,求
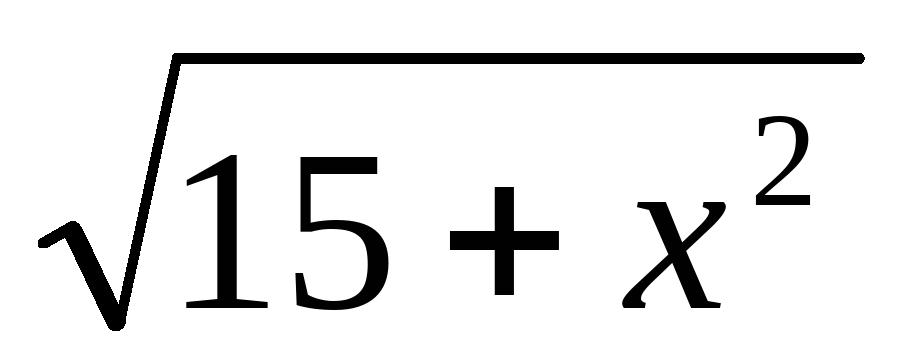
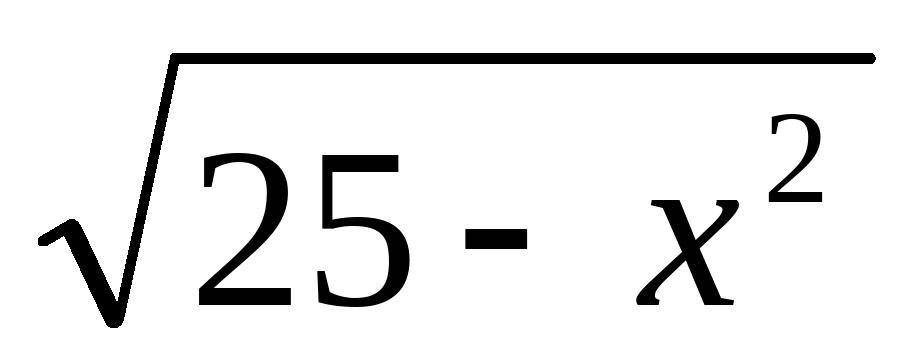 的值18、已知关于x的一元二次方程x2 2(k-1)x k2-1= 0有两个不相等的实数根.(1)求实数k的取值范围;(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.19、在等腰△ABC中,三边分别为
的值18、已知关于x的一元二次方程x2 2(k-1)x k2-1= 0有两个不相等的实数根.(1)求实数k的取值范围;(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.19、在等腰△ABC中,三边分别为
 、
、
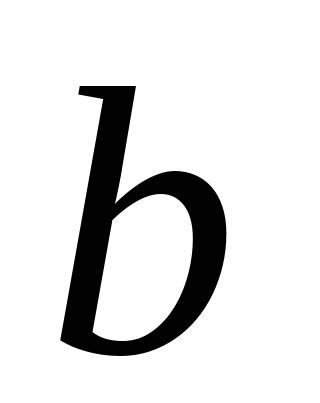 、
、
 ,其中
,其中
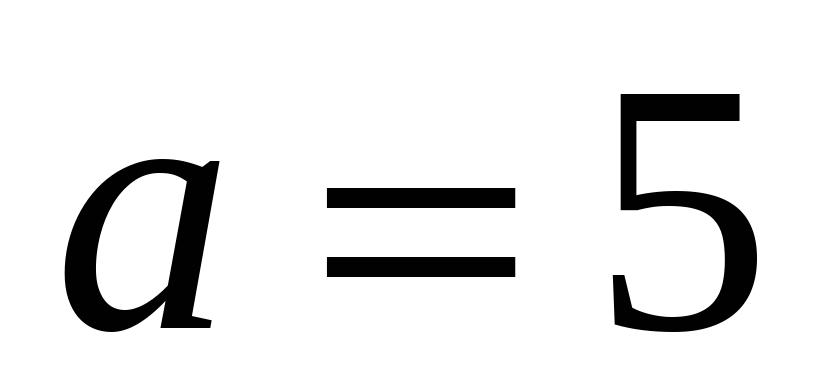 ,若关于
,若关于
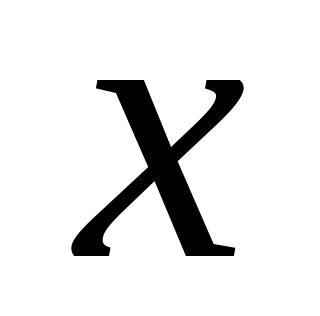 的方程
的方程
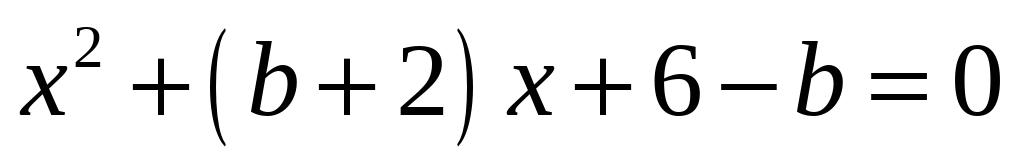 有两个相等的实数根,求△ABC的周长.20、关于
有两个相等的实数根,求△ABC的周长.20、关于
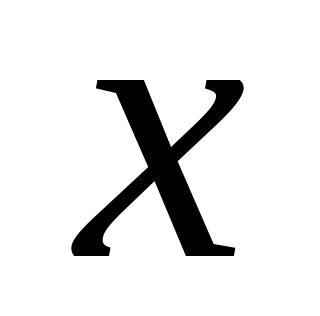 的一元二次方程
的一元二次方程
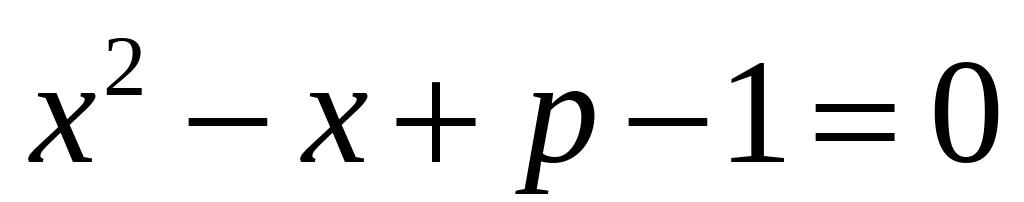 有两实数根
有两实数根
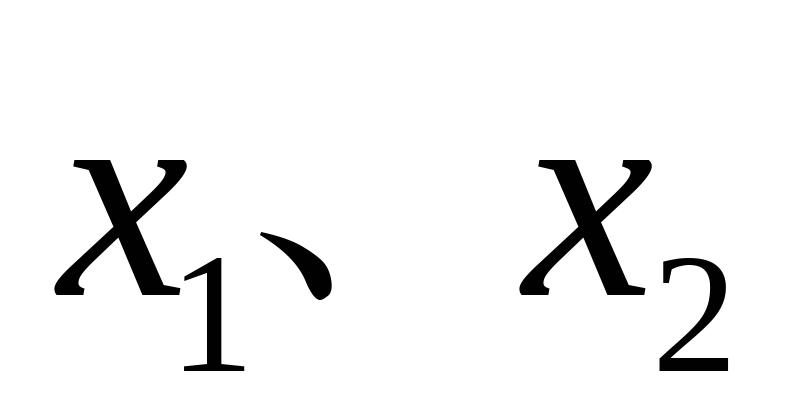 .(1)求
.(1)求
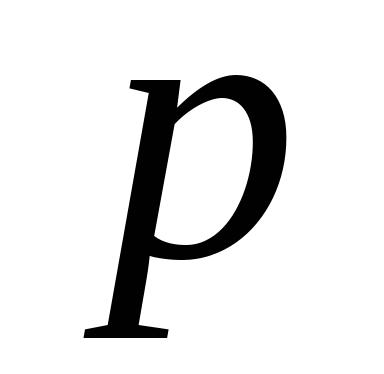 的取值范围;(2)若
的取值范围;(2)若
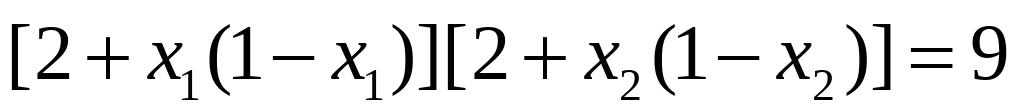 ,求
,求
 的值.1、益群精品店以每件21元的价格购进一批商品,该商品可以自行定价,若每件商品售价a元,则可卖出(350-10a)件,但物价局限定每件商品的利润不得超过20%,商店计划要盈利400元,需要进货多少件?每件商品应定价多少?
的值.1、益群精品店以每件21元的价格购进一批商品,该商品可以自行定价,若每件商品售价a元,则可卖出(350-10a)件,但物价局限定每件商品的利润不得超过20%,商店计划要盈利400元,需要进货多少件?每件商品应定价多少?
2、一个醉汉拿着一根竹竿进城,横着怎么也拿不进去,量竹竿长比城门宽4米,旁边一个醉汉嘲笑他,你没看城门高吗,竖着拿就可以进去啦,结果竖着比城门高2米,二人没办法,只好请教聪明人,聪明人教他们二人沿着门的对角斜着拿,二人一试,不多不少刚好进城,你知道竹竿有多长吗?3、一个长为10m的梯子斜靠在墙上,梯子的底端距墙角6m.(1)若梯子的顶端下滑1m,求梯子的底端水平滑动多少米?(2)若梯子的底端水平向外滑动1m,梯子的顶端滑动多少米?(3)如果梯子顶端向下滑动的距离等于底端向外滑动的距离,那么滑动的距离是多少米?4

、如图所示,我海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D恰好位于AC的中点,岛上有一补给码头;小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航.一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送往军舰.(1)小岛D和小岛F相距多少海里?(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?5、如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道
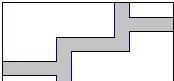
路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540平方米,则道路的宽为________ 米.6、阅读材料:设一元二次方程
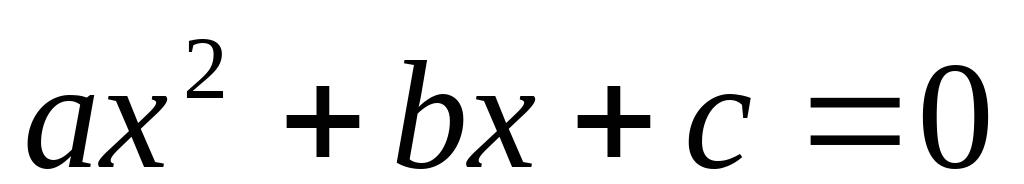 (
(
 ≠0)的两根为
≠0)的两根为
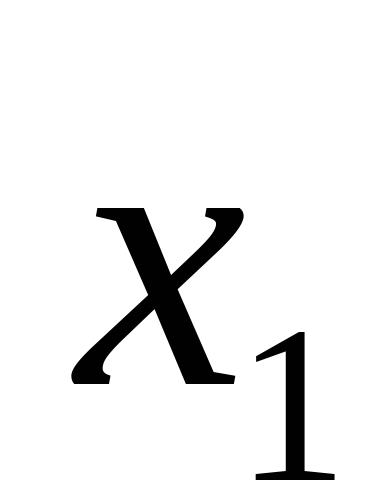 ,
,
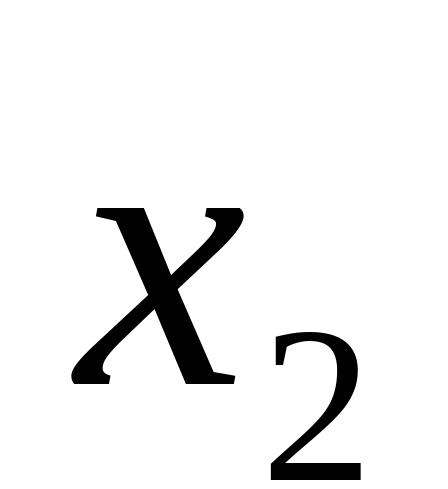 ,则两根与方程的系数之间有如下关系:
,则两根与方程的系数之间有如下关系:
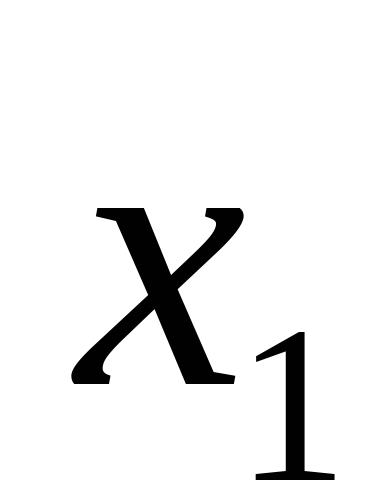
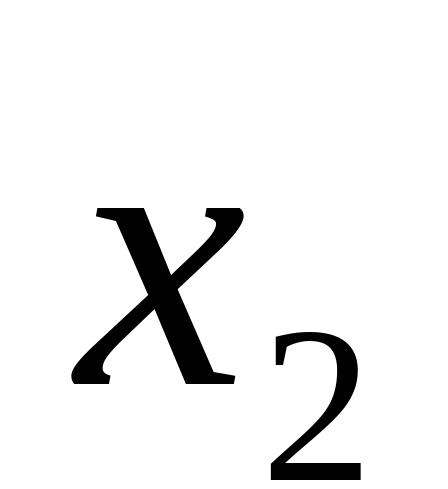 =-
=-
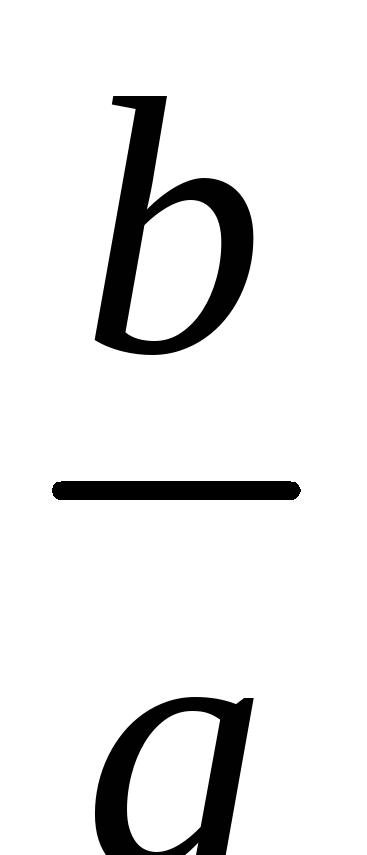 ,
,
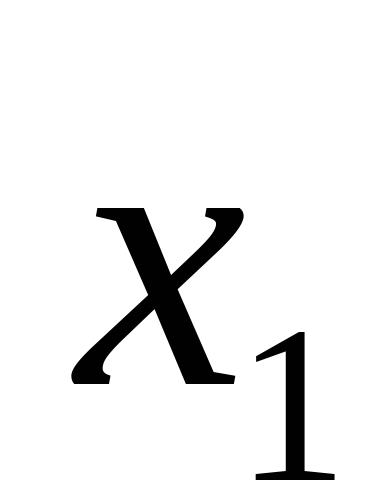 ·
·
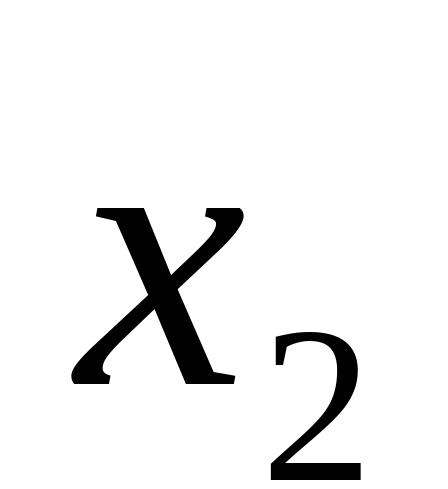 =
=
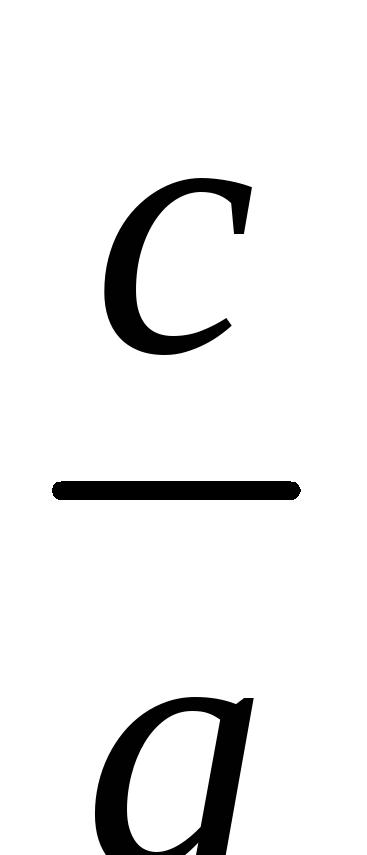 .根据该材料完成下列填空:已知
.根据该材料完成下列填空:已知
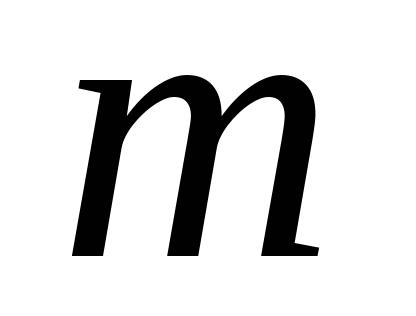 ,
,
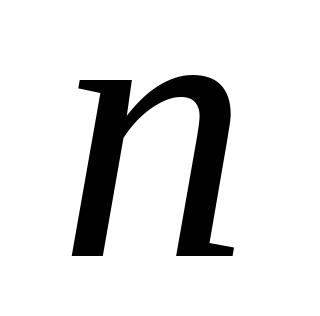 是方程
是方程
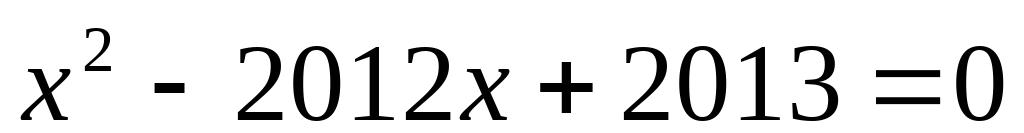 的两根,则(1)
的两根,则(1)
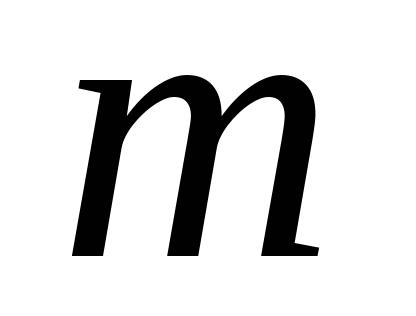
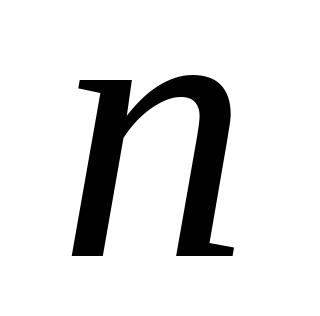 = ,
= ,
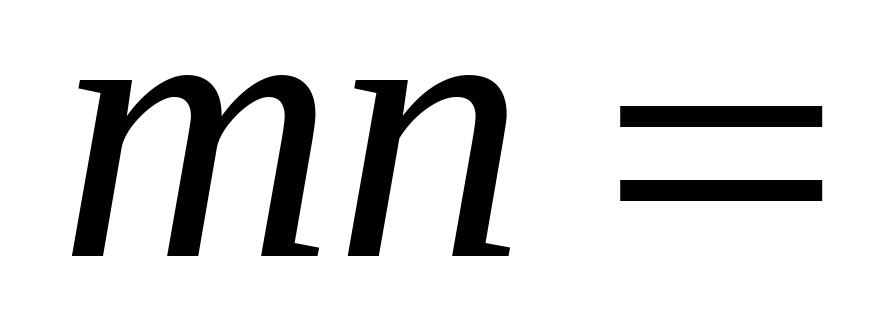 ;(2)(
;(2)(
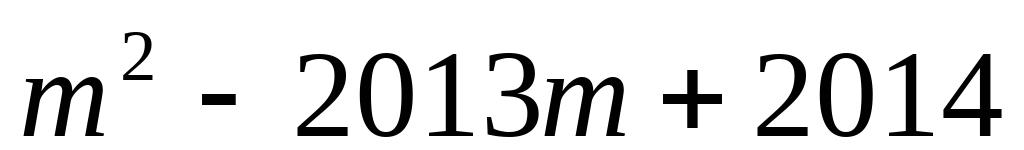 )(
)(
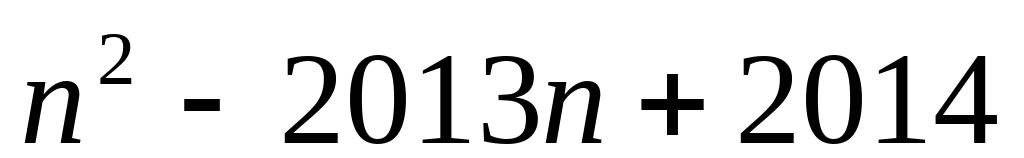 )= .7、我市“利民快餐店”试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本).若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价x(元)取整数,用y(元)表示该店日纯收入.(日纯收入=每天的销售额﹣套餐成本﹣每天固定支出)(1)若每份套餐售价不超过10元.①试写出y与x的函数关系式;②若要使该店每天的纯收入不少于800元,则每份套餐的售价应不低于多少元?(2)该店既要吸引顾客,使每天销售量较大,又要有较高的日纯收入.按此要求,每份套餐的售价应定为多少元?此时日纯收入为多少元?8、某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)求每台A型电脑和B型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2
)= .7、我市“利民快餐店”试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本).若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价x(元)取整数,用y(元)表示该店日纯收入.(日纯收入=每天的销售额﹣套餐成本﹣每天固定支出)(1)若每份套餐售价不超过10元.①试写出y与x的函数关系式;②若要使该店每天的纯收入不少于800元,则每份套餐的售价应不低于多少元?(2)该店既要吸引顾客,使每天销售量较大,又要有较高的日纯收入.按此要求,每份套餐的售价应定为多少元?此时日纯收入为多少元?8、某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)求每台A型电脑和B型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2
 倍。设购进A掀电脑x台,这100台电脑的销售总利润为y元。①求y与x的关系式;②该商店购进A型、B型各多少台,才能使销售利润最大?(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案。9、解方程:(1)
倍。设购进A掀电脑x台,这100台电脑的销售总利润为y元。①求y与x的关系式;②该商店购进A型、B型各多少台,才能使销售利润最大?(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案。9、解方程:(1)
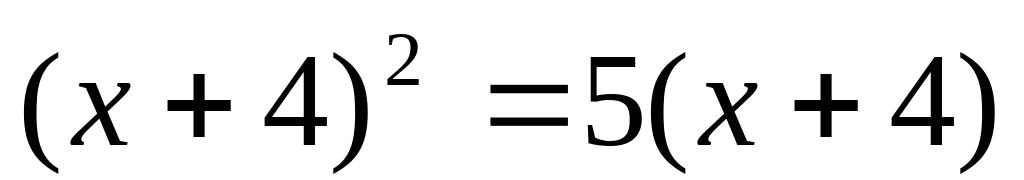 (2)
(2)
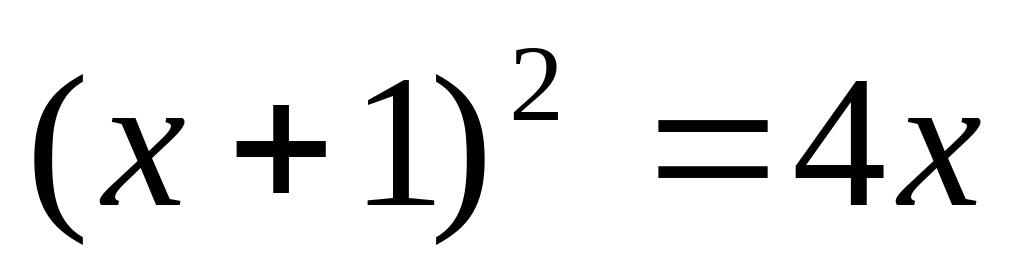 (3)
(3)
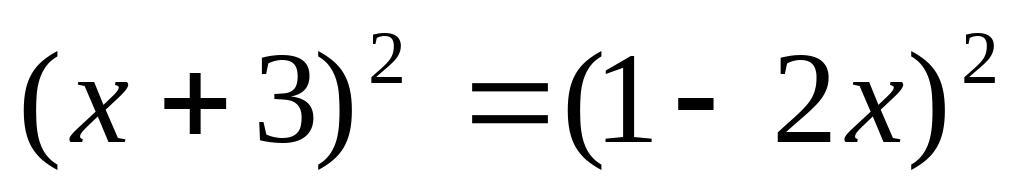 (4)
(4)
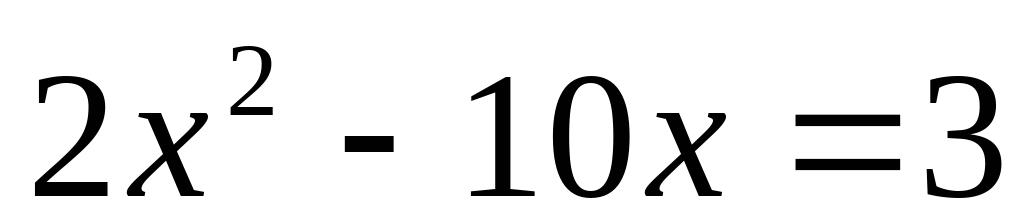 (5)
(5)
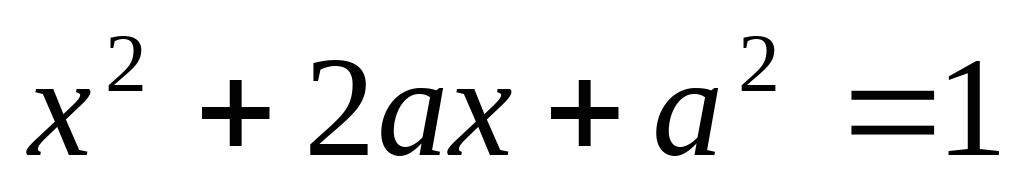 (6)
(6)
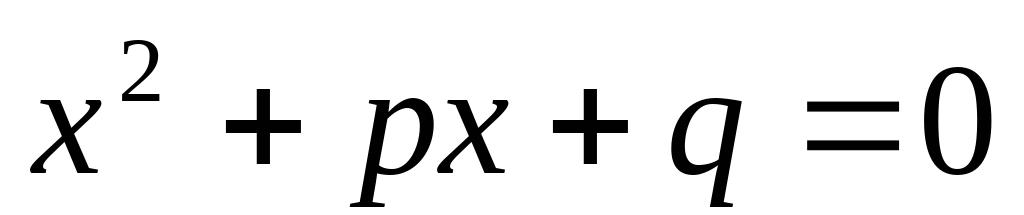 10、阅读下面的例题:解方程
10、阅读下面的例题:解方程
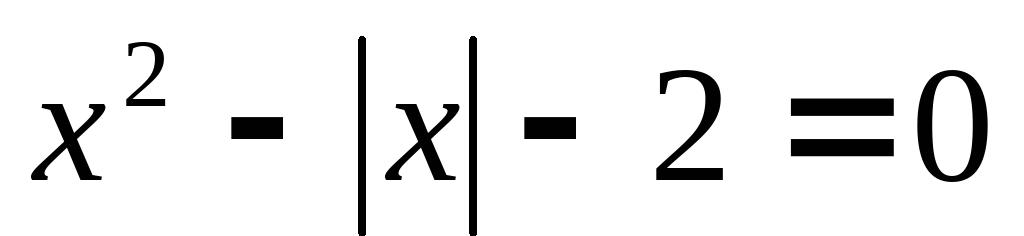 解:当x≥0时,原方程化为x2– x –2=0,解得:x1=2,x2=- 1(不合题意,舍去)当x<0时,原方程化为x2 x –2=0,解得:x1=1,(不合题意,舍去)x2=-2∴原方程的根是x1=2,x2=- 2 。请参照例题解方程
解:当x≥0时,原方程化为x2– x –2=0,解得:x1=2,x2=- 1(不合题意,舍去)当x<0时,原方程化为x2 x –2=0,解得:x1=1,(不合题意,舍去)x2=-2∴原方程的根是x1=2,x2=- 2 。请参照例题解方程
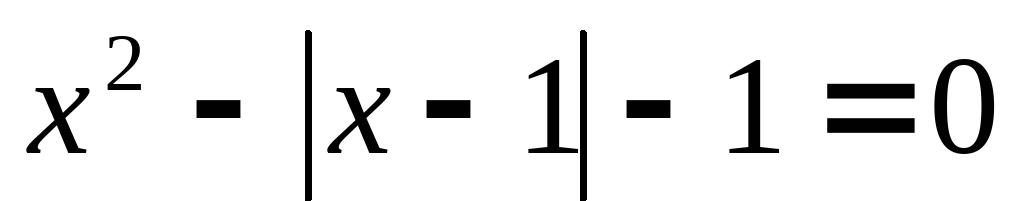
温馨提示
《中小学微学堂》,由江苏省数学名师、数学奥林匹克国家级教练员,联手四名特级教师共同打造。
微
 七年级数学微课大全
七年级数学微课大全
课
 八年级数学微课大全
八年级数学微课大全
集
 完整版!中考数学复习大全
完整版!中考数学复习大全