转动惯量与角速度的乘积是什么?
1.1、转动惯量乘以角加速度是表示转动刚体的动量矩。
2、平动中的牛顿第二定律:F=ma,合外力=质量×线加速度。转动中,就成了M=Iβ;合外力矩=转动惯量×角加速度。
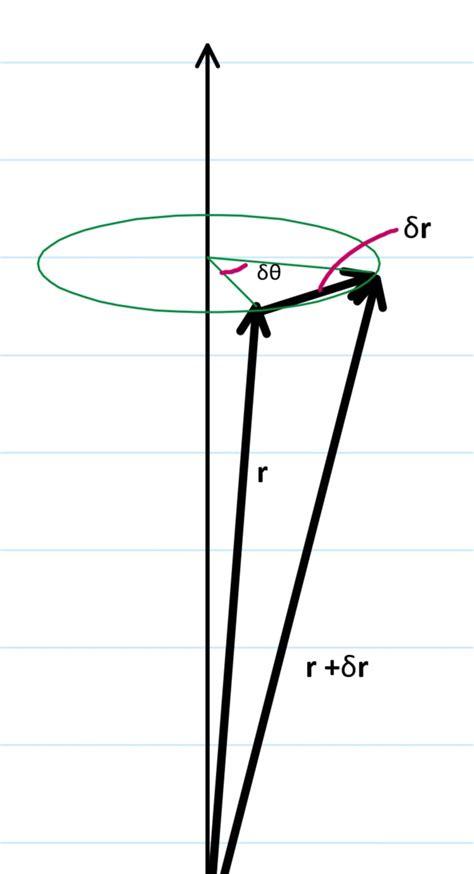
3、平动中,牛顿第二定律的动量表述:合外力=线动量的变化率;线动量=质量×速度。转动中,牛顿第二定律的角动量表述:合外力矩=角动量的变化率;角动量=转动惯量×角速度。
4、平动中的动能:Ek=??mv??=??质量×线速率的平方。转动中的动能Ek=??mv??=??转动惯量×角速率的平方。
根据转动定律:刚体所受的力矩M与刚体的转动惯量I以及刚体的角加速度B的关系是:M=I*B。
此定律的物理意义是:若刚体的转动惯量一定,刚体所受的力矩越大它获得的角加速度也越大。
转动惯量与转动角速度没有直接关系。转动惯量和角加速度可以用转动定律联系起来,力矩等于转动惯量乘以角加速度。然后,角加速度对时间积分可以求出角速度。
转动惯量定义是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。其量值取决于物体的形状、质量分布及转轴的位置。可说是一个物体对于旋转运动的惯性。对于一个质点,I=mr^2,其中m是其质量,r是质点和转轴的垂直距离。转动惯量在旋转动力学中的角色相当于线性动力学中的质量,描述角动量、角速度、力矩和角加速度等数个量之间的关系。转动惯量的表达式为I=∑mi*ri^动量是与物体的质量和速度相关的物理量。一般而言,一个物体的动量指的是这个物体在它运动方向上保持运动的趋势。动量公式p=m·v区别:转动惯量是绕轴运动的惯性量,而动量是运动方向上保持的运动趋势。
转动惯量乘以角速度等于什么?
1.转动惯量乘以角加速度是表示转动刚体的动量矩。
平动中的牛顿第二定律:F = ma,合外力 = 质量× 线加速度。转动中,就成了 M = Iβ;合外力矩 = 转动惯量× 角加速度。
平动中,牛顿第二定律的动量表述:合外力 = 线动量的变化率;线动量 = 质量× 速度。转动中,牛顿第二定律的角动量表述:合外力矩 = 角动量的变化率;角动量 = 转动惯量× 角速度。
平动中的动能:Ek =?? mv?? = ?? 质量 × 线速率的平方。 转动中的动能 Ek =?? mv?? =?? 转动惯量 × 角速率的平方。
扩展资料:
一个质量为m、速度为v、矢径为r的质点对r的原点的动量矩为L=r×mv。动量矩是个矢量,它在某一轴上的投影就是对该轴的动量矩。对轴的动量矩是个标量。质点系或刚体对某点(或某轴)的动量矩等于其中所有质点的动量对该点(或该轴)之矩的矢量和(或代数和)。
平动的刚体,由于它的各点的速度都相同(见刚体的平动),所以它对某点的动量矩等于刚体质心以该点为原点的矢径与刚体动量的矢量积。一个作半径r的匀速圆周运动的质点绕圆心O转动的角速度为),则质点对O的动量矩即质点的角动量。
2.转动惯量与转动角速度没有直接关系。转动惯量和角加速度可以用转动定律联系起来,M=Ja,力矩等于转动惯量乘以角加速度。然后,角加速度对时间积分可以求出角速度。
转动周数时(例如:每分钟转动周数),则以转速来描述转动速度快慢。角速度的方向垂直于转动平面,可通过右手螺旋定则来确定。
为ω=dφ/dt,而速度的垂直分量等于;其中θ是向量r与v的夹角,则导出,在二维坐标系中,角速度是一个只有大小没有有方向的伪纯量,而非纯量。纯量与伪纯量不同的地方在于,当轴与轴对调时,纯量不会因此而改变正负符号,然而伪纯量却会因此而改变。