前不久,笔者撰写了Matlab偏微分工具箱的使用与案例实操,今天继续讲解偏微分方程数字详解和实例程序,希望能够对Matlab学习者有些许帮助。
一、写在前面
一般而言,偏微分方程解析求解只有在定解问题比较简单,求解区域比较规则条件下才有可能应用,可解决问题的局限性比较大。实际工程问题中遇到的情况都比较复杂,或由于边界不规则,解析解方法比较困难,大多数问题需采用数值解法。偏微分方程有多种数值解法,如有限差分法、正交配置法、线上法(MOL)、有限元法等,本期过冷水就和大家详细了解一下数值方法的具体原理和实用案例。
线上法指将偏微分方程仅有一个自变量保持连续,而将其它变量进行离散,从而把偏微分方程转变为常微分方程组进行求解的数值方法。通常线上法选择离散的自变量是空间变量,而将时间变量保持连续,离散方法可以选择有限差分法或配置法。
考虑一维扩散方程:
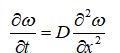
其中扩散系数D为常数。将空间变量x采用差分法进行离散。令:
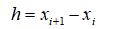
则:
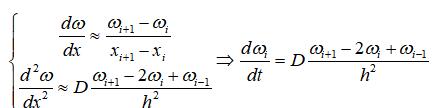
由于转化过程中,原方程的边界条件被包含在离散化过程中,原方程变为常微分方程组的初值问题求解。
对于二维过程的离散也类似,例如,二维扩散方程;
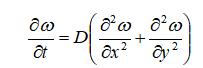
离散:
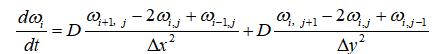
讲完数值解的离散方法后,求解偏微分方程的具体实现程序。
二、Pdepe函数求解偏微分方程
pdepe函数用于求解如下类型问题:
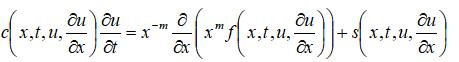
满足条件:
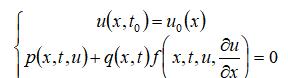
pdepe函数调用格式
sol= pdepe(m,pdepe,icfun,bcfun,xmesh, tspan)sol = pdepe(m,pdepe,icfun,bcfun,xmesh,tspan,options)sol = pdepe(m,pdepe,icfun,bcfun,xmesh,tspan,options,p1,p2,…)m表示级数, m=0,1,2分别代表平板、圆柱和球形。
pdefun是描述偏微分方程的函数,其格式为[c,f,s]=pdefun( x,t,u,dudx)。输出变量c,f,s是列向量,输人变量x和 t为标量,表示空间和时间的自变量,u和dudx分别是问题的解u(x,t)和它对x的偏导数的近似。
icfun描述定解问题初始条件的函数,其格式为u=icfun(x)。icfun计算和返回解的初始值。
bcfun是描述定解问题边界条件的函数,格式为[pl,ql,pr,qr]= bcfun( xl,ul,xr,ur,t)。其中ul是在左边界xl=α处的近似解,ur是在右边界xr=b处的近似解。pl和ql是p和q在xl处的列向量值,同样pr和qr是p和q在xr处的列向量值。当m>0和 a=0时﹐解的有界性要求通量f在a=0处为0, pdepe 会自动处理,并忽略pl和ql的值。
xmesh是空间变量x的网点向量, pdepe不会自动选择。xmesh=[x0,xl,…,xn],满足 x0<x1<…<xn,且 x….的长度必须大于3, xmesh(1)=a和 xmesh(end)=b.。pdepe的求解效率与x..的选择好坏关系很大。通常在梯度较大处应加密网格。
tspan是时间变量t 的网点向量,是用户在该处想得到数值解的时间向量。tspan—[t0,t1,…,tn],满足t0<tl<…<tf,且 t.span的长度必须大于3,tspan( 1)=t0和tspan(end)=tf。求解效率和 tspan的疏密关系不大。
sol是一个三维数组,存放数值解。sol(:,:,i)=ui是解向量的第i个分量。sol(j,k,i)=u(j,k)是解向量ui在(x,t)=(tspan(j),xmesh(k))处的数值解。sol(j,:.i)是解向量第i个分向量ui在时间 t.span(j)和网格点xmesh(:)处的数值解。
options是 MATLAB常微分方程求解函数( pdepe函数需调用ode15s进行时间积分)options 的一部分,如RelTol,AbsTol,NormControl,InitiaIStep 和 MaxStep。一般不用调整options 的值即可获得满意的解,如果需要改变则可以采用odeset 函数,这与常微分方程求解是相同的。
p1.p2,…是通过pdepe传递给pdefun,icfun和 bcfun的参数。
三、案例演示
1、对于一维扩散问题
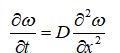
边界条件:
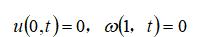
初始条件:

当D=1时,试求解以上方程,采用图形将计算结果输出,并与x = 0.3,t = 0.005、0.01、0.02的精确解0.5966、0.5799、0.5334比较。
根据函数可求得图像为:
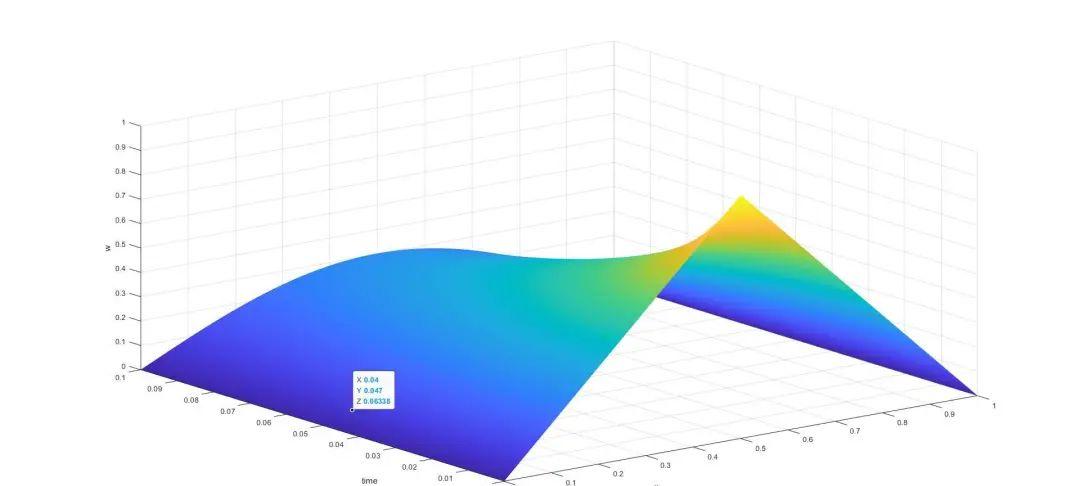
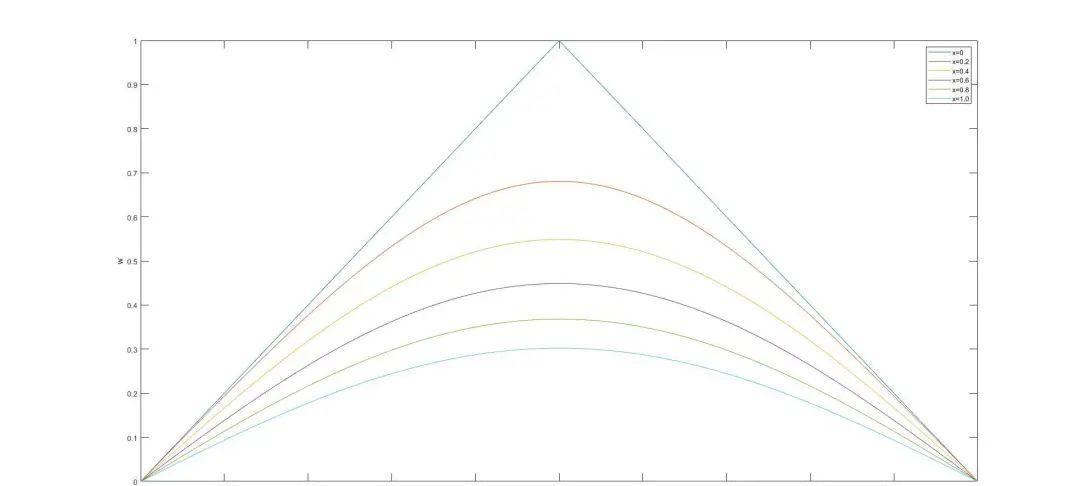
pdepe求解程序为:
function pdem=0;xmesh= 0:0.01:1;tspan=0:0.001:0.1;sol = pdepe(m,@pdefun,@icfun,@bcfun,xmesh,tspan);surf( xmesh,tspan,sol)xlabel(‘x’), ylabel(‘time’), zlabel(‘w’);shading interpfigureplot( tspan,sol(1:20:101,:))xlabel(‘time’)ylabel(‘w’)legend(‘x=0′,’x=0.2′,’x=0.4′,’x=0.6′,’x=0.8′,’x=1.0’)disp(‘The anlytic results for t=0.005 0.01 0.02 @x=0.3 are;’ )disp([0.5966 0.5799 0.5334])disp(‘The corresponding results obtained from pdepe are:’)disp([sol(6,31),sol( 11,31),sol(21,31)])function [c,f,s]= pdefun(x,t,u,du) c= 1; D=1; f=D*du; s=0;endfunction u=icfun(x) if x>=0&x<=1/2 u=2*x; elseif x>=1/2&x<=1 u=2*(1-x); endendfunction [pl,ql,pr,qr]= bcfun(xl,ul,xr,ur,t) pl = ul; ql =0; pr = ur; qr=0;endend该结果相对来说还算是满意的,在调试过程中过冷水发现在偏微分计算中函数调用形式和以前接触的方法有点不同,使用起来不太习惯,调试花费了好久时间,看来知识还需要精进。
接下来,过冷水分享几个实用案例,瞬态热传导、牛顿流体方程、固定床二维均相模型。
2、瞬态热传导
针对这样一个问题:
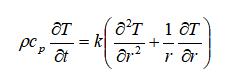
边界条件:
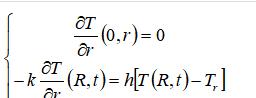
初始条件:
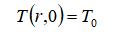
已知:
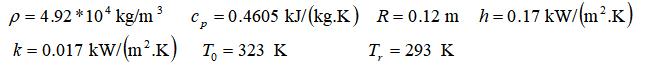
原方程可化为标准形式:
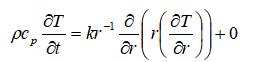
据此求解程序如下:
function pdeglobal h k rho Cp Trh=0.17;k=0.017;T0=323;Tr=293;rho=4.92*10^4;Cp=0.4605;R=0.12;m=1;rmesh=linspace(0,R,30);tspan=0:0.001:0.1;sol = pdepe(m,@pdefun,@icfun,@bcfun,rmesh,tspan);surf( rmesh,tspan,sol)xlabel(‘r’), ylabel(‘time’), zlabel(‘Temperature’);shading interpcolormap coolfunction [c,f,s]= pdefun(x,t,u,du) c=rho*Cp; f=k*du; s=0;endfunction u=icfun(x) T0=323; u=T0endfunction [pl,ql,pr,qr]= bcfun(xl,ul,xr,ur,t) pl = ul; ql =0; pr =h*( ur-Tr); qr=k;endend
结果为:
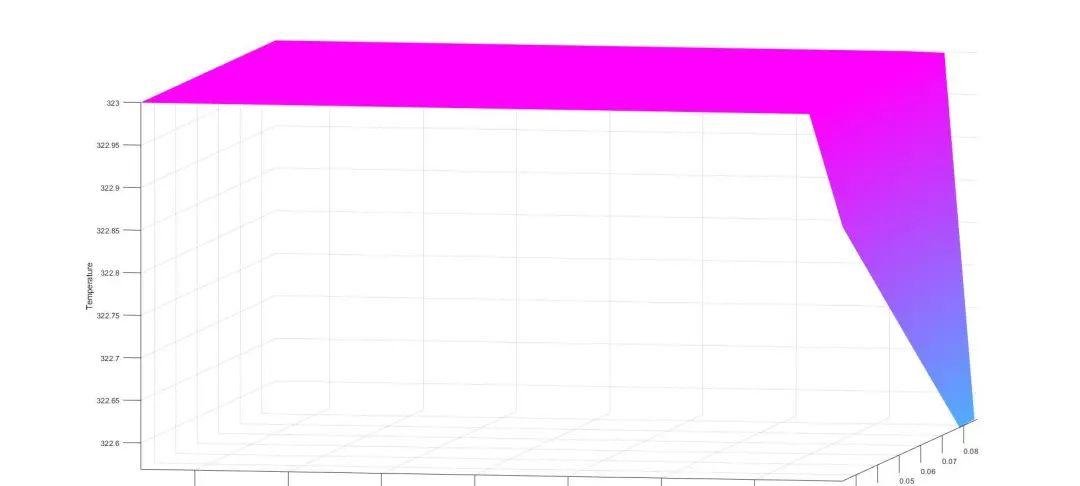
3、牛顿流体运动方程
水平圆管中装有静止的牛顿流体﹐从某个时刻起外加压力△p,流体开始流动,以采用如下方程描述:
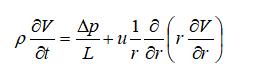
边界条件:
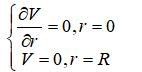
初始条件:
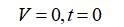
已知:
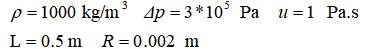
程序:
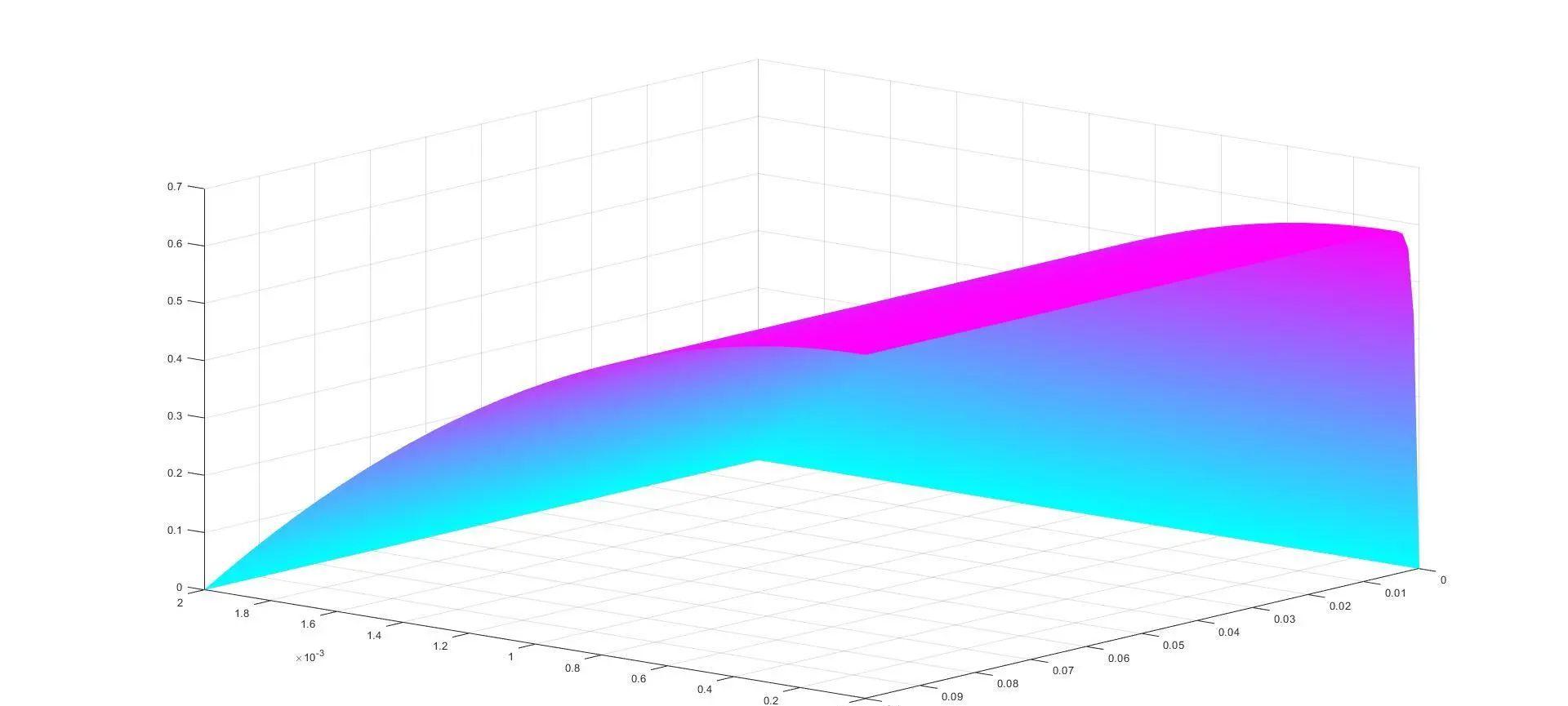
function pdeglobal rho miu deltPrho=1000;miu=1;L=0.5;dP=3*10^5;deltP=dP/L;R=0.002;m=1;rmesh=linspace(0,R,30);tspan=0:0.001:0.1;sol = pdepe(m,@pdefun,@icfun,@bcfun,rmesh,tspan);surf( rmesh,tspan,sol)shading interpcolormap coolpp=pchip(sol(:,1),tspan);SF=0.98*sol(end,1);ST=ppval(pp,SF);function [c,f,s]= pdefun(x,t,u,du) c=rho; f=miu*du; s=deltP;endfunction u=icfun(x) u=0endfunction [pl,ql,pr,qr]= bcfun(xl,ul,xr,ur,t) pl = ul; ql =0; pr =ur; qr=0;endend结果为:
4、固定床均相模型
在固定床反应器中进行乙烯催化氧化制备环氧乙烷反应,如果忽略环氧乙烷的燃烧反应,则反应器内进行的反应如下。
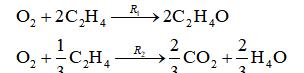
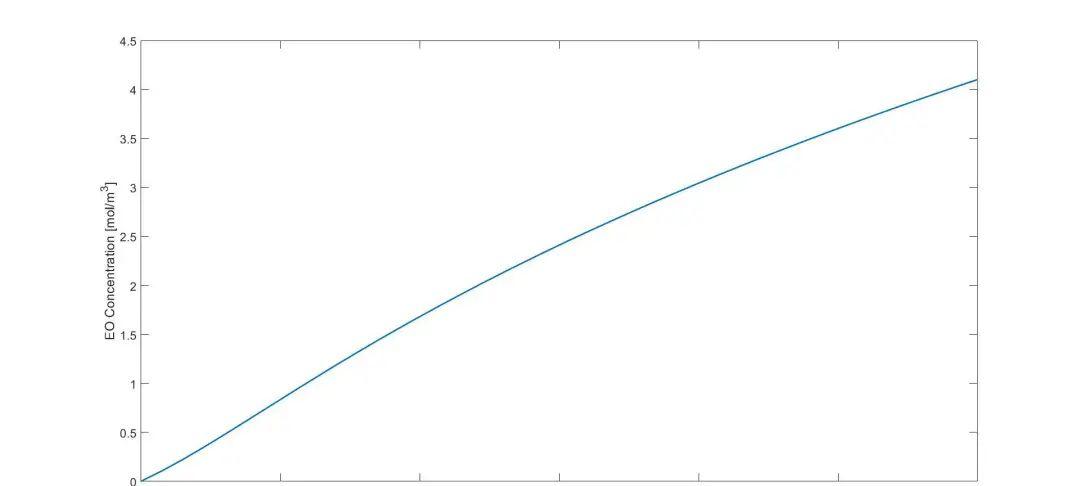
采用二维拟均相反应器模型进行模拟,求产物环氧乙烷浓度和反应器温度沿反应器管长的变化。反应器模型可构建为:
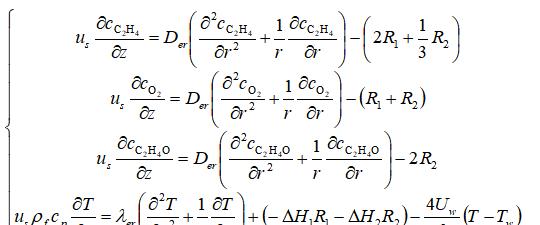
初始条件:
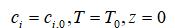
边界条件:
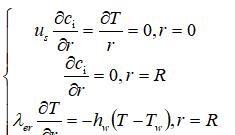
其中Der和λer分别为流体径向有效扩散和传热系数,数值分别为Der=6×10-4 m2 /s,λer= 0.1 J/(m2· s.K); hw为反应器器壁的导热系数,其值为250 J/(m2· s ·K);
源程序为:
dt=0.0508;Tw=498;L=12;rmesh=linspace(0,dt,10);tspan=linspace(0,L,40);m=1;sol = pdepe(m,@pdefun,@icfun,@bcfun,rmesh,tspan);%求不同床层位置的平均温度和产物浓度CEO=sol(:,:,3);T=sol(:,:,4);[row,col]=size(CEO);for i=1:rowcpp=pchip(rmesh,CEO(i,:));cav(i)=quadl(@ppval,rmesh(1),dt,[],[],cpp)./dt;tpp=pchip(rmesh,T(i,:));Tav(i)=quad(@ppval,rmesh(1),dt,[],[],tpp)/dt;endplot(tspan,cav,’Linewidth’,2);xlabel(‘Bed Length [m]’,’fontsize’,16)ylabel(‘EO Concentration [mol/m^3]’,’fontsize’,16)set(gca,’Fontsize’,16)figureplot( tspan,Tav,’linewidth’,2);xlabel(‘Bed Length [m]’,’fontsize’,16);ylabel ( ‘Bed Temperature [K]’,’fontsize’,16)set(gca,’Fontsize’,16)function C=icfun(r)C=[224,14,0,498];endfunction [c,f,s]= pdefun(r,z,C,dCdr)dt=0.0508;Tw=498;CEH=C(1);CO2=C(2);CEO=C(3);T=C(4);us= 1.3;rhouf = 6.06;cp= 1160 ;Uw=270;Der= 6e-4;lbr=0.1;dH1=-210000;dH2=-473000;R=8.314 ;k1= 35.2 * exp( -59860/R/T);k2= 24700 * exp(-89791/R/T);R1=810 *k1*CO2;R2=2430* k2*CO2;c=[us/Der;us/Der;us/Der;us*rhouf*cp/lbr];f=[dCdr(1); dCdr(2); dCdr(3); dCdr(4)];s=[-(2*R1 1/3*R2)/Der;-(R1 R2)/Der;2*R1/Der;((-dH1*R1-dH2*R2)-4*Uw*(T-Tw)/dt)/lbr];endfunction [pl,ql,pr,qr]= bcfun(rl,ul,rr,ur,z)dt=0.0508;Tw=498;hw =250;lbr=0.6;pl =[0;0;0;0];ql=[1;1;1;1];pr =[0;0:0;-hw*(ur-Tw)/lbr];%pr =[0;0;0;0];qr=[1;1;1;1];end
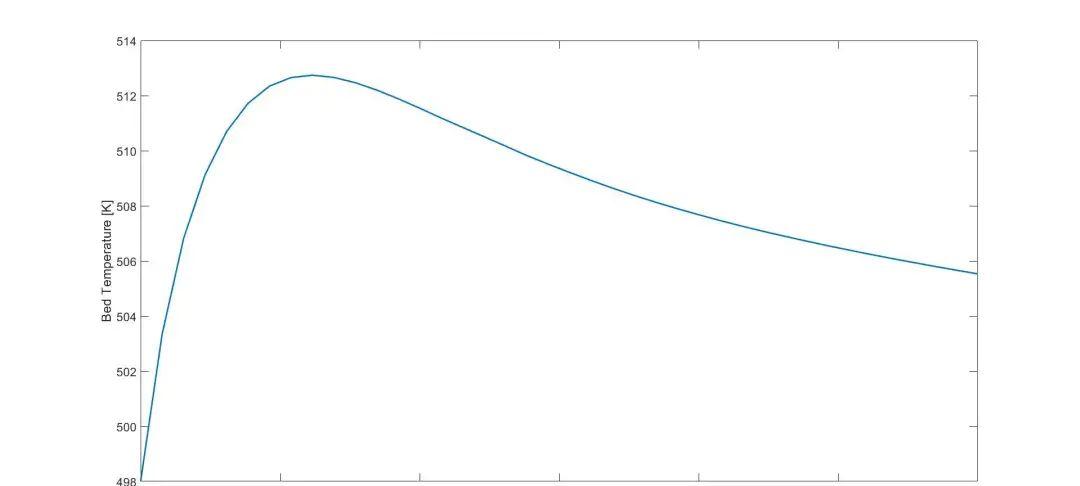
(完)
相关阅读
Matlab仿真圈资料库:“硬件光阴”的资源导航过冷水:浅析数模大赛实用的Matlab六大图像处理技巧原程序过冷水:教你学习图像matlab加密处理方法过冷水:送你Matlab数据转换图和一套读取储存代码
过冷水:分子动力学数据的Matlab处理程序设计(附学习资料)