小思考
刚刚遇到小明,问了他一个问题: 给你一个数字数组,找出最小的数字,怎么整?

小明:Array.sort!
我:如果这个数组是动态的,每次我都要找最小值,找到之后就从数组里删除这个元素,然后下次还想找最小值,怎么整。并且这个过程中,还会不断有新的数字插入数组。
小明:Array.sort!
我:可是数组是动态的,每次sort,但是我只要最小值,你浪费那么多时间把第二和第一万都排那么准确,不觉得在浪费时间吗?
小明:好像确实是浪费时间。可能是个算法吧,没做过。
React中的任务池
其实这不是个纯算法题,说回React,大家肯定听过React中有个fiber任务吧,而且不同的fiber任务有不同的优先级,为了用户体验,React需要先处理优先级高的任务。
为了存储这些任务,React中有两个任务池,源码中定义如下:
// Tasks are stored on a min heapvar taskQueue = [];var timerQueue = [];
taskQueue与timerQueue都是数组,前者存储的是立即要执行的任务,而后者存的则是可以延迟执行的任务。
源码中任务的初始结构定义如下:
var newTask = { id: taskIdCounter , // 标记任务id callback, // 回调函数 priorityLevel, // 任务优先级 startTime, // 任务开始时间,时间点 expirationTime, // 过期时间,时间点 sortIndex: -1, // 任务排序,取值来自过期时间,因此值越小,优先级越高 };
React中一旦来了新任务,就会先用currentTime记录当前时间(performance.now()或者Date.now()),如果任务有delay参数,那么任务开始执行时间startTime = currentTime delay;。接下来通过startTime > currentTime如果成立,证明任务是可以延期的,那么任务进入timerQueue,否则进入taskQueue。
React中的任务调度
那么问题来了,怎么找到优先级最高的任务呢,以taskQueue为例,它是动态的任务池,数据形式上就是个数组。Array.sort可行,但不是最优方案,每次sort,平均时间复杂度高达nlog(n)。这个时候我们需要了解个数据结构:最小堆,也叫小顶堆。
当然可能有人问了,为什么不是最大堆呢?这是因为taskQueue的newTask中的排序用的是sortIndex,这个值取自过期时间expirationTime,也就意味着优先级越高的任务越需要立马执行,那么过期时间自然也就越小了,换句话说就是,优先级越高,过期时间越小。当然有可能两个任务的过期时间一样,那这个时候就要看是谁先进的任务池了,也就是newTask中的id嘛,每次来了新任务,id都会加1。因此React源码中任务比较优先级的函数如下:
function compare(a, b) { // Compare sort index first, then task id. const diff = a.sortIndex – b.sortIndex; return diff !== 0 ? diff : a.id – b.id;}
其实用到最小堆,也就是把taskQueue做成最小堆的数据结构,然后执行任务的时候,取最小堆的最小任务,如果任务执行完毕,那么需要把这个任务从taskQueue中删除,并重新调整剩下的任务池,依然保证它是最小堆的数据结构。当然,往taskQueue中插入新任务的时候,也要调整taskQueue,保证新的任务池仍然是最小堆。
最小堆
了解最小堆之前,先来熟悉三个基本数据结构的概念:
二叉树
是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
从图形形态上看,满二叉树外观上是一个三角形。
如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
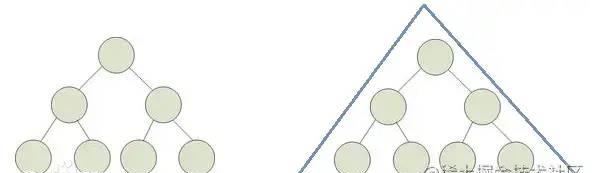
注意: 关于满二叉树定义这里,国内外定义有分歧,本文采用的是国内定义。满二叉树英文是Full Binary Tree,是指所有的节点的度只能是0或者2。
如下图,国外也认为是Full Binary Tree:
而对于我们本文所说的满二叉树,国外的概念叫完美二叉树。
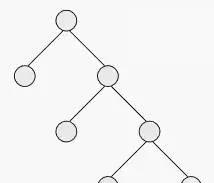
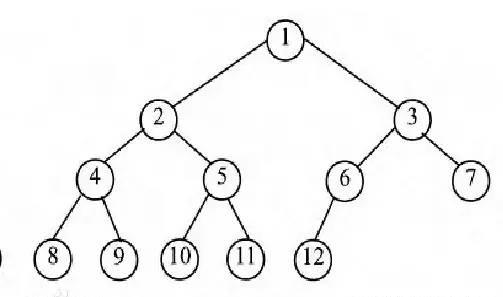
完全二叉树
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。叶子结点只可能在最大的两层出现。
最小堆
是一种经过排序的完全二叉树,其中任一非终端节点的数据值均不大于其左子节点和右子节点的值。
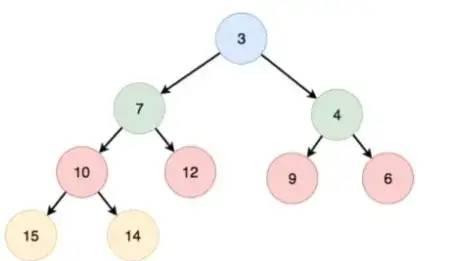
如对于上面这个最小堆来说,经过观察,对应的深度与数组下标分别是:

经过观察,发现父子节点下标关系如下:
根据子节点下标推算父节点下标:parentIndex = (childIndex – 1) >>> 1
根据父节点下标推算子节点下标:
leftIndex = (index 1 )2 – 1,
rightIndex = leftIndex 1
至此,我们就可以尝试去实现最小堆的增(push)删(pop)查(peek)函数了:
peek
peek,瞄一下嘛,即获取最小堆的堆顶值。
export function peek(heap) { return heap.length === 0 ? null : heap[0];}push
往最小堆中添加一个元素,因为taskQueue本身已经是最小堆,并且是数组存储,这时候为了尽可能多的复用原先的结构,我们可以先把新元素插入数组尾部,然后从下往上调整最小堆:
export function push(heap, node) { const index = heap.length; heap.push(node); siftUp(heap, node, index);}
怎么从下往上调整呢?因为最小堆的典型特点就是父节点比左右子节点都小,那这时候除了尾部元素,其他都是满足这个特点的。这个时候我们只需要调整尾部元素以及和尾部元素的祖先就可以了,一直往上调整,直到不再需要调整为止。代码如下:
// 向上调整最小堆function siftUp(heap, node, i) { let index = i; while (index > 0) { // 父节点下标 const parentIndex = (index – 1) >>> 1; // 父节点 const parent = heap[parentIndex]; if (compare(parent, node) > 0) { // parent>node, 不符合最小堆 heap[parentIndex] = node; heap[index] = parent; index = parentIndex; } else { // 已经符合最小堆,上面的祖先本身就是最小堆结构,因此停止调整 return; } }}pop
删除堆顶元素。即React一个任务执行完了,那么肯定要把这个任务从任务池taskQueue中删除。问题来了,怎么删除呢,堆顶元素其实就是taskQueue[0],这个位置我们肯定还是要用的,并且和push一样,为了尽可能复用原先的最小堆结构,我们可以采取一个办法:把最后一个元素覆盖堆顶元素,然后从堆顶往下调整最小堆。
export function pop(heap) { if (heap.length === 0) { return null; } const first = heap[0]; const last = heap.pop(); // 如果堆顶和堆尾元素不相等,证明现在的元素总数>1,需要往下调整 if (first !== last) { heap[0] = last; siftDown(heap, last, 0); } return first;}
关于往下调整,其实就是检查每个子堆的结构,确保最小值在父节点,不满足就交换父与左或者父与右,代码如下,我加了尽可能多的详细注释:
function siftDown(heap, node, i) { let index = i; const len = heap.length; const halfLen = len >>> 1; while (index < halfLen) { let leftIndex = (index 1) * 2 – 1; let left = heap[leftIndex]; let rightIndex = leftIndex 1; let right = heap[rightIndex]; // todo 比较parent与left与right的大小 // 如果parent不是最小的,那就比较left和right谁最小,然后把最小的和parent交换位置 // 如果parent是最小的,那就停止 if (compare(left, node) < 0) { // left < parent // 为了保证根节点最小,比较left和right if (rightIndex < len && compare(right, left) < 0) { // right<left, right是最小的,交换parent和right heap[index] = right; heap[rightIndex] = node; index = rightIndex; } else { // right>left, left是最小的,交换parent和left heap[index] = left; heap[leftIndex] = node; index = leftIndex; } } else if (rightIndex < len && compare(right, node) < 0) { // left > parent // 检查right, right<parent heap[index] = right; heap[rightIndex] = node; index = rightIndex; } else { // parnent最小 return; } }}总结
至此,相信大家都已经学会了React任务调度与最小堆。