log函数意义是什么?
1.如果a^b=c,则称b是以a为底c的对数,记作:b=loga(c)。
loga(a)=1,loga(a^x)=x(x是任意一个实数),在一般情形下,loga(c)需要查表或用计算器才能得到结果的近似值,如果你有常用对数表(以10为底)或自然对数表(以e为底),可以用换底公式分别用lg(c)/lg(a)或ln(c)/ln(a)来计算loga(c)的近似值,计算器也要用这两个式子来计算loga(c)的近似值
log在数学中是指对数函数。
“log”是“logarithm”的缩写,是对数函数的意思。常写作函数 y=log(a) x,意思是数x叫做以a为底N的对数。对数和幂运算是相对的,常用的对数函数以10为底的对数,记为lg、以无理数e为底,记为ln。
??
扩展资料:
对数在数学内外有许多应用。这些事件中的一些与尺度不变性的概念有关。例如,鹦鹉螺的壳的每个室是下一个的大致副本,由常数因子缩放。这引起了对数螺旋。Benford关于领先数字分配的定律也可以通过尺度不变性来解释。
对数也与自相似性相关。例如,对数算法出现在算法分析中,通过将算法分解为两个类似的较小问题并修补其解决方案来解决问题。自相似几何形状的尺寸,即其部分类似于整体图像的形状也基于对数。对数刻度对于量化与其绝对差异相反的值的相对变化是有用的。
此外,由于对数函数log(x)对于大的x而言增长非常缓慢,所以使用对数标度来压缩大规模科学数据。对数也出现在许多科学公式中,例如Tsiolkovsky火箭方程,Fenske方程或能斯特方程。
对数函数图像及性质总结?
1.对数函数的一般形式为
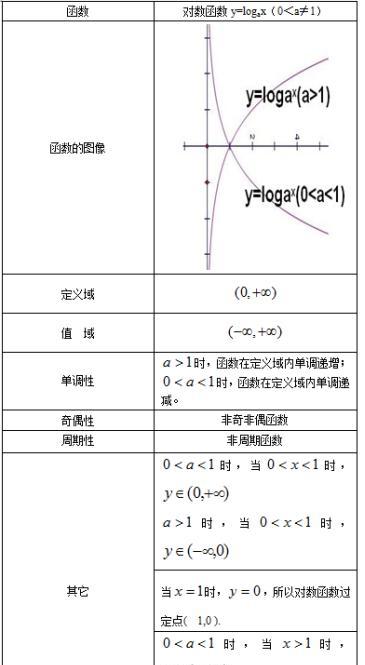
,它实际上就是指数函数的反函数。因此指数函数里对于a的规定,同样适用于对数函数。
对于不同大小a所表示的函数图形:
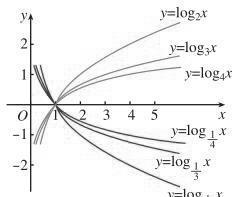
可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形,因为它们互为反函数。
(1)对数函数的定义域为大于0的实数集合。
(2)对数函数的值域为全部实数集合。
(3)函数总是通过(1,0)这点。
(4)a大于1时,为单调递增函数,并且上凸;a小于1大于0时,函数为单调递减函数,并且下凹。
(5)显然对数函数无界。
性质:定义域求对数函数y=loga x 的定义域是{x |x>0},但如果遇到对数型复合函数的定义域的求解,除了要注意真数大于0以外,还应注意底数大于0且不等于1,如求函数y=logx(2x-1)的定义域,需满足{x>0且x≠1} .
{2x-1>0 =〉x>1/2且x≠1,即其定义域为 {x |x>1/2且x≠1}值域:实数集R
定点:函数图像恒过定点(1,0).
单调性:a>1时,在定义域上为单调增函数,并且上凸;
0<a<1时,在定义域上为单调减函数,并且下凹.
奇偶性:非奇非偶函数,或者称没有奇偶性.
周期性:不是周期函数
零点:x=1
注意:负数和0没有对数.