怎么求多项式的次数和项数?
1.项数的定义:多项式中的每个单项式叫做多项式的项。
次数的定义:这些单项式中的最高项次数,就是这个多项式的次数。
多项式的系数:是一类组合数,是多项式的展开式中,项的系数。
例如:3xy+4a+5b,这是一个多项式,
它的项数是3,分别是3xy、4a、5b。系数分别是3、4、5。

1、一个多项式中,次数最高的项的次数,叫做这个多项式的次数。
2、xy的项数与次数:项数是1,次数是2 (因为字母可以看做1x×1y 这里的数是1)
例如:x的2次方—3x+2的次数是2,2a的2次方(乘)b+3b—1的次数是3。
3、由定义决定:一个多项式中次数最高的单项式的次数即为此多项式的次数。
4、对于比较广义的定义,1个或0个单项式的和也算多项式。
5、按这个定义,多项式就是整式。
6、实际上,还没有一个只对狭义多项式起作用,对单项式不起作用的定理。
7、0作为多项式时,次数定义为负无穷大(或0)。
8、单项式和多项式统称为整式。
9、多项式中不含字母的项叫做常数项。
10、如:5X+6中的6就是常数项。
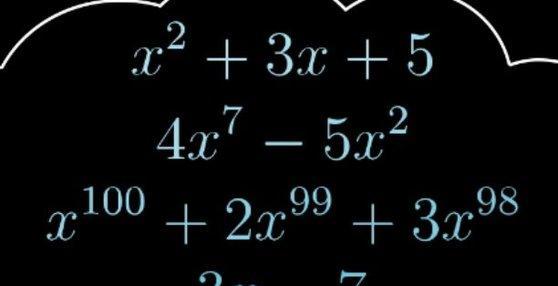
1.单项式
(1)单项式的概念:数与字母的积这样的代数式叫做单项式,单独一个数或一个字母也是单项式。
注意:数与字母之间是乘积关系。
(2)单项式的系数:单项式中的字母因数叫做单项式的系数。
如果一个单项式,只含有字母因数,是正数的单项式系数为1,是负数的单项式系数为—1。
(3)单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
2.多项式
(1)、多项式的概念:几个单项式的和叫做多项式。在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。一个多项式有几项就叫做几项式。多项式中的符号,看作各项的性质符号。
(2)、多项式的次数:多项式中,次数最高的项的次数,就是这个多项式的次数。
(3)、多项式的排列:
a.把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
b.把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
由于多项式是几个单项式的和,所以可以用加法的运算定律,来交换各项的位置,而保持原多项式的值不变。 为了便于多项式的计算,通常总是把一个多项式,按照一定的顺序,整理成整洁简单的形式,这就是多项式的排列。
3.合并同类项
(1)、合并同类项的概念:
把多项式中的同类项合并成一项叫做合并同类项。
(2)、合并同类项的法则:
同类项的系数相加,所得结果作为系数,字母和字母的指数不变。
(3)、合并同类项步骤:
a、准确的找出同类项。
b、逆用分配律,把同类项的系数加在一起(用小括号),字母和字母的指数不变。
c、写出合并后的结果。