python一元线性回归分析代码(python线性回归实例)-昊阳知识网

简书专栏：

https://www.jianshu.com/u/2f376f777ef1

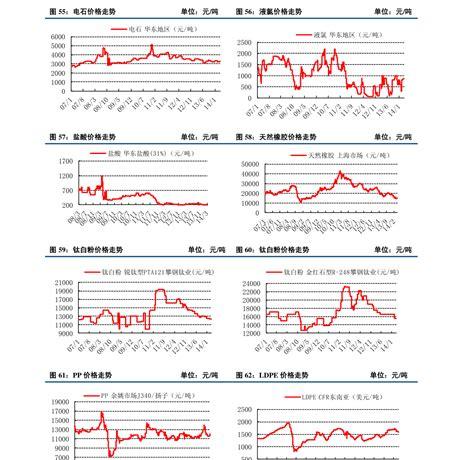
编者注：本文包含了使用Python2.X读取数据、数据处理、作图，构建梯度下降法函数求解一元线性回归，并对结果进行可视化展示，是非常综合的一篇文章，包含了Python的数据操作、可视化与机器学习等内容。学习了这一篇文章就大概了解或掌握相关Python编程与数据分析等内容。另外，本文还巧妙地进行了一个设计，这使得本文Python代码也可用于多元线性回归，这是区别与现有网络上大多数梯度下降法求解线性回归的Python实现不同，具体会在文中说明。一、梯度下降法与回归分析梯度下降法则是一种最优化算法，它是用迭代的方法求解目标函数得到最优解，是在cost function（成本函数）的基础上，利用梯度迭代求出局部最优解。在这里关于梯度下降法不做过多介绍，相关资料已经很多且后边还会结合构建的函数进行分析，借用网上常用的一个比喻去直观解释。比如，我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。回归在数学上来说是给定一个点集，能够用一条曲线去拟合之，如果这个曲线是一条直线，那就被称为线性回归，线性回归大家应该很熟悉，在这里也不过多解释，后边构造代码的时候也会去分析一些，在回归分析中，只包括一个自变量和一个因变量，即y=a bx u称为一元线性回归分析。若是包含多个因变量则是多元线性回归，即y=a b1x1 b2x2 … bnxn u。二、用Python读取所要使用的数据数据来自于UCI的机器学习数据库中的Auto-mpg汽车燃料效率（mpg），共有398个样本，以及9个变量，分别是mpg（燃料效率）、cylinders（发动机里的气缸数量）、displacement（发动机的位移）、horsepower（发动机的马力，有缺失值）、weight（汽车的重量）、acceleration（汽车的加速性能）、model year（汽车类型的生产年份）、car name（汽车品牌）等等。在导入numpy、pandas、matplotlib、math等数据处理相关模块后，通过读取url来导入数据，部分数据网页呈现形式截图如下：

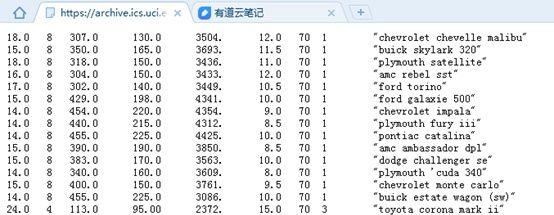
网页数据呈现形式有两个需要注意的地方（这也是许多UCI数据的特点）：一是没有表头，我们就在代码中构建name列表并加入pd.read_csv中，否则的话数据第一行就会作为表头；二是数据间用空格来间隔，我们就在pd.read_cs加入delim_whitespace=True来分列，默认分隔符为逗号。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math

url = ‘https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data’
names =[“mpg”,”cylinders”,”displacement”,”horsepower”,
“weight”,”acceleration”,”model year”,”origin”,”car name”]
cars = pd.read_csv(url, delim_whitespace=True,names=names)#值与值之间，使用空白字符来指定你想要的分隔符
cars.head(5)

得到结果：

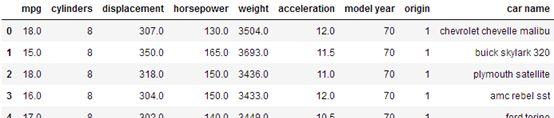
对其中的mpg与acceleration绘制散点图如下：

plt.scatter(cars[“mpg”] ,cars[“acceleration”]) #mpg燃料效率；acceleration汽车的加速性能
plt.xlabel(‘mpg’)
plt.ylabel(‘acceleration’)#设置坐标轴标签
plt.show()

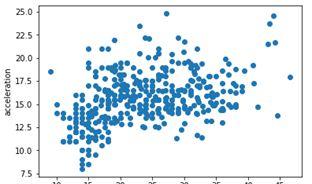
三、数据处理——构建X、Y变量

将’mpg’,’weight’列单独拿出来，作为构建回归分析的X、Y变量，代码如下：

data = cars[[‘mpg’,’acceleration’]]#选取表格中的’mpg’,’weight’列
data.insert(0, ‘Ones’, 1) #在data第1-2列之间插入全是1的一列数
# set X (training data) and y (target variable)
cols = data.shape[1] #计算data的列数，在这里cols为3
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]

在这里可能很多人会有疑问：为什么要插入一列全是1的数据？为什么还要采用iloc选取列的函数来重新定义X、y，本文分析的变量’mpg’,’weight’不是已经有了么？因此，在这里我们需要对回归分析模型着重说一下。事实上，无论是一元线性回归如y=β0 β1x，还是多元线性回归如y=β0 β1×1 β2×2 … βnxn u，都可以用矩阵形式表示：

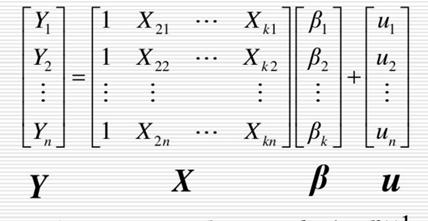
对于一元线性回归，那么上数矩阵就是取k=2，X变量也就是前两列，即1和X21—X2n的矩阵，这就是为什么要在data中插入全是1的一列意义所在，然后用iloc选取前两列为X变量，最后一列为y变量。四、先用最小二乘法求解回归并计算损失函数为了比较梯度下降法的求解结果，在这里先用最小二乘法求解回归，具体求解过程不再细述，其求解公式为：

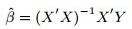
线性回归的平方差损失函数为：

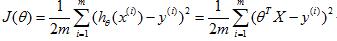
代码如下

X = np.matrix(X.values)
y = np.matrix(y.values) #首先要把变量由data frames 转变为矩阵形式
from numpy.linalg import inv
from numpy import dot
theta_n = dot(dot(inv(dot(X.T, X)), X.T), y) # theta = (X’X)^(-1)X’Y
print theta_n

def computeCost(X, y, theta):
inner = np.power(((X * theta.T) – y), 2)
return np.sum(inner) / (2 * len(X))
X.shape, theta_n.shape, y.shape
lr_cost = computeCost(X, y, theta_n.T)
print(lr_cost)

Machine Learning Exercises In Python,Part 1,

http://www.johnwittenauer.net/machine-learning-exercises-in-python-part-1/**

（吴恩达笔记 1-3）——损失函数及梯度下降http://blog.csdn.net/wearge/article/details/77073142?locationNum=9&fps=1**

梯度下降法求解线性回归之python实现http://blog.csdn.net/just_do_it_123/article/details/51056260